100% tevredenheidsgarantie Direct beschikbaar na betaling Zowel online als in PDF Je zit nergens aan vast
logo-home
Eerder door jou gezocht
Eerder door jou gezocht
logo
Summary of Continuum Physics €4,49
In winkelwagen
Snel navigeren naar
Voorbeeld
  2.  
  3. Technische Universiteit Delft (TU Delft)
  4.  
  5. Continuum Physics (AP3032)

Samenvatting

Summary of Continuum Physics
 11 keer bekeken  0 keer verkocht

This document covers all the subjects and equations of the course of continuum physics. If you understand this document, then the course will be a breeze.

Voorbeeld 2 van de 10  pagina's

Document informatie

  • Nee
  • 1-7
  • 31 januari 2023
  • 10
  • 2022/2023
  • Samenvatting

Onderwerpen

Gekoppeld boek

book image

Titel boek:

Auteur(s):

  • Uitgave:
  • ISBN:
  • Druk:

Geschreven voor

Alle documenten voor dit vak (1)

Verkoper

avatar-seller
jonathanpilgram

Voorbeeld van de inhoud

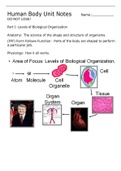
Summary continuum physics
Jonathan Pilgram
January 25, 2023


1 The stress and strain tensor
All small x are the deformed coordinates and all big X are the material coordinates (before de-
formation).


1.1 Deformation gradient
∂xi
Fij =
∂Xj


1.2 Tangent vectors
∂xi
Gi = e
∂Xj i
With ei being unit base vectors.


1.3 Displacement vector
ui = xi − Xi


1.4 Greens strain tensor
1 ∂ui ∂uj ∂uk ∂uk
Eij = ( + + )
2 ∂Xj ∂Xi ∂Xi ∂Xj


1.5 Infinitesimal strain tensor
Also known as linear or Cauchy strain tensor. Coordinate system is interchangeable as the dif-
ferences are very small.
1 ∂ui ∂uj
ϵij = ( + )
2 ∂Xj ∂Xi

1.5.1 Compatibility equation for 2D infinitesimal strain tensor
∂ 2 ϵ11 ∂ 2 ϵ22 ∂ ∂
2 + −2 ϵ12 = 0
∂x2 ∂x21 ∂x1 ∂x2




1

, 1.5.2 Compatibility equations for 3D infinitesimal strain tensor
∂ 2 ϵ11 ∂ 2 ϵ22 ∂ ∂
2 + −2 ϵ12 = 0
∂x2 ∂x21 ∂x1 ∂x2
∂ 2 ϵ22 ∂ 2 ϵ33 ∂ ∂
2 + −2 ϵ23 = 0
∂x3 ∂x22 ∂x2 ∂x3
∂ 2 ϵ11 ∂ 2 ϵ33 ∂ ∂
2 + 2 −2 ϵ13 = 0
∂x3 ∂x1 ∂x1 ∂x3
∂ ∂ϵ23 ∂ϵ31 ∂ϵ12 ∂ ∂
(− + + )− ϵ11 = 0
∂x1 ∂x1 ∂x2 ∂x3 ∂x2 ∂x3
∂ ∂ϵ23 ∂ϵ31 ∂ϵ12 ∂ ∂
( − + )− ϵ22 = 0
∂x2 ∂x1 ∂x2 ∂x3 ∂x3 ∂x1
∂ ∂ϵ23 ∂ϵ31 ∂ϵ12 ∂ ∂
( + − )− ϵ33 = 0
∂x3 ∂x1 ∂x2 ∂x3 ∂x1 ∂x2

1.6 Velocity field in Eulerian and Lagrangian description
Given a Lagrangian description of a flow field as:

X(x0 , t)

And Eulerian description of a flow field as:

u(x, t)

Then they are related by:
∂X
u(X(x0 , t), t) = (x0 , t)
∂t

1.7 Line segment length
(ds)2 − (dS)2 = Eij xi xj
With ds being the infinitesimal line segment after transformation and dS being infinitesimal line
segment before transformation.


1.8 Principal values stress tensor
The principal values of the stress tensor are the solution to the eigenvalue problem:

|σ − Iλ| = 0

If you order these principal values as as σI > σII > σIII , then the maximum shear stress is given
by:
σIII − σI
σs,max = ±
2
Now one can draw Mohr’s circles by putting down the principal stress values on a horizontal nor-
mal stress axis. The shear stress will then by the vertical axis. Then draw three circles between
the points.




2

Voordelen van het kopen van samenvattingen bij Stuvia op een rij:

Verzekerd van kwaliteit door reviews

Verzekerd van kwaliteit door reviews

Stuvia-klanten hebben meer dan 700.000 samenvattingen beoordeeld. Zo weet je zeker dat je de beste documenten koopt!

Snel en makkelijk kopen

Snel en makkelijk kopen

Je betaalt supersnel en eenmalig met iDeal, creditcard of Stuvia-tegoed voor de samenvatting. Zonder lidmaatschap.

Focus op de essentie

Focus op de essentie

Samenvattingen worden geschreven voor en door anderen. Daarom zijn de samenvattingen altijd betrouwbaar en actueel. Zo kom je snel tot de kern!

Veelgestelde vragen

Wat krijg ik als ik dit document koop?

Je krijgt een PDF, die direct beschikbaar is na je aankoop. Het gekochte document is altijd, overal en oneindig toegankelijk via je profiel.

Tevredenheidsgarantie: hoe werkt dat?

Onze tevredenheidsgarantie zorgt ervoor dat je altijd een studiedocument vindt dat goed bij je past. Je vult een formulier in en onze klantenservice regelt de rest.

Van wie koop ik deze samenvatting?

Stuvia is een marktplaats, je koop dit document dus niet van ons, maar van verkoper jonathanpilgram. Stuvia faciliteert de betaling aan de verkoper.

Zit ik meteen vast aan een abonnement?

Nee, je koopt alleen deze samenvatting voor €4,49. Je zit daarna nergens aan vast.

Is Stuvia te vertrouwen?

4,6 sterren op Google & Trustpilot (+1000 reviews)

Afgelopen 30 dagen zijn er 55628 samenvattingen verkocht

Opgericht in 2010, al 14 jaar dé plek om samenvattingen te kopen

Start met verkopen
€4,49
  • (0)
In winkelwagen
Toegevoegd