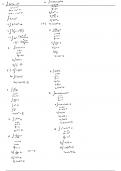Antiderivatives Study guides, Class notes & Summaries

Section 17 - Antiderivatives and Indefinite Integrals- Calc 143- MAT143

Antiderivatives (Indefinite Integrals) solved questions

This document is high level overview of topics such as EVT, First Derivative Test, Antiderivative rules, and Concavity with examples.

Summary based on coursework in the Engineering Maths 115 course at Stellenbosch University. Used for Tutoring Purposes on Teachme2.

Before we introduce double integration, let us recall the fact that for functions of a single variable, integration is the reverse process of differentiation. Also see examples below. Functions of a Single Real Variable Functions of Two Real Variables Functions of Two Real Variables differentiation. 6) where ≠ −1 . 7) One of the antiderivatives of Thus we have . 8) The general form of antiderivativ denoted by where

Examples of antiderivatives to look over

Comprehensive Class notes on the fundamental theorem of calculus antiderivatives/integration with examples Based on CLP 2 textbook

extreme value theorem - Correct Answer if f(x) is continuous on [a,b] then f(x) contains an absolute max and absolute min on [a,b] Fermat's theorem - Correct Answer if f(x) is differentiable on (a,b) and has a local max or min at c within (a,b), then f'(c) = 0 critical points - Correct Answer for f(x), point a at which either f'(a) = 0 or f is not differentiable at a (closed intervals include endpoints) mean value theorem - Correct Answer if f(x) is continuous on [a,b] and differenti...

evaluate the integral 2/1, ln(x)/x dx - answer-(ln2)^2/2 consider the function f(x)=x^4-4x^3. which of the following is NOT true - answer-f has a local extrema at x=0 and x=3 find the work done by a force F=sqroot 2x+1 N to move an object along a straight path from a distance of 0 meters to a distance of 4 meters - answer-26/3 J an object is moving along the x-axis. Let s(t), v(t) and a(t) be functions giving the position, the velocity, and the acceleration of the object at time t. whic...