Newton-Raphson
Some equations are impossible to solve using techniques from Core Maths.
Newton’s method, also known as the Newton-Raphson method, helps to approximate the real
zeros (roots) of a function. It uses tangent lines to approximate the graph of the function near its
x-intercepts.
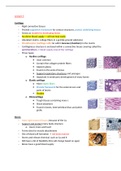
Refer to the graph:
To solve f (x) = 0
Let us say x = a certain value, a
Step 1: Make a guess, a1, ‘close to’ the required solution.
Step 2: Find the equation of the tangent y = f (x) at point P (a1; f (a1)):
. - Get the derivative of the function and sub in a point.
. - m = f ‘(a1)
. - point on the graph (a1; f (a1))
. = Equation: y – f (a1) = f ‘(a1)( x – a1)
Step 3: Calculate the x-intercept of this tangent:
. - Make y = 0 ad solve the equation of the tangent.
. - f(a1) = f ‘(a1)(x – a1)
𝑓(𝑎1 )
. - + a1 = x
𝑓′(𝑎1 )
Step 4: Use the above calculated x as your a2
Step 5: Use a2 as your new guess and continue the process (iteration) until the solution is
. repeated to the required number of decimals.
𝑓(𝑥𝑛 ) 𝑦 𝑣𝑎𝑙𝑢𝑒
Formula: xn+1 = xn - ( )
𝑓′(𝑥𝑛 ) 𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒
, Newton-Raphson does NOT always work
1. f must be differentiable on some interval containing the roots.
2. If f ‘(x) = 0 for some n, the tangent is horizontal and the next approximation can’t be
calculated.
3. If the first approximation is not carefully chosen, the approximation can oscillate between 2
values.
4. If f ‘(x) is close to 0, the second approximation could be worse and you would move further
away from the root.