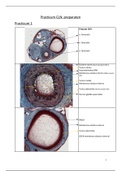
SOLUTION MANUAL
SOLUTION MANUAL
,Chapter 1 1-1
Chapter 1 Solutions
1.1 Part (c) is false. The predicted value of Y when X = 2 is Ŷ = 100 + 15(2) = 130, not 110.
Parts (a), (b), and (d) are true.
1.2 A residual plot does not help assess (c) the condition of independence of the residuals. It does
help assess (a) linearity, (b) constant variance, and (d) zero mean.
1.3 The slope is given in the output under the heading Coef for the predictor W ingLength. The
estimate is β̂1 = 0.4674.
1.4 The slope is given in the output under the heading Coef for the predictor Y ear. The estimate
is β̂1 = 0.01251.
1.5 The intercept is given in the output under the heading Coef for the Constant. The estimate
is β̂0 = 1.3655.
1.6 The intercept is given in the output under the heading Coef for the Constant. The estimate
is β̂0 = −16.47.
1.7 As wing length increases by 1 mm, the weight increases by 0.4674 g, on average.
1.8 As year increases by 1, the length of the winning long jump increases by 0.01251 m, on average.
1.9 The regression standard error is given in the output as S = 1.39959. We can also compute
this from the information given in the Error row of the Analysis of Variance:
SSE 223.31 √
σˆE = = = 1.959 = 1.39959
n−2 116 − 2
A typical deviation of a sparrow weight from the line predicted by its wing length might be about
1.4 grams.
1.10 The regression standard error is given in the output as S = 0.259522. We can also compute
this from the information given in the Error row of the Analysis of Variance:
SSE 1.751 √
σˆE = = = 0.06735 = 0.2595
n−2 28 − 2
A typical deviation of a winning Olympic long jump length from the line predicted by its year
might be about 0.26 meters.
1.11 The degrees of freedom for the regression standard error are n − 2 = 116 − 2 = 114. The
value also appears in the DF column of the Analysis of Variance section of the output.
,1-2 Chapter 1
1.12 The degrees of freedom for the regression standard error are n − 2 = 28 − 2 = 26. The value
also appears in the DF column of the Analysis of Variance section of the output.
1.13 The predicted value is ŷ1 = 25 + 7(10) = 95. The residual is y1 − ŷ1 = 100 − 95 = 5.
1.14 The predicted value is ŷ1 = 78 − 0.5(30) = 63. The residual is y1 − ŷ1 = 60 − 63 = −3.
1.15 ˆ = 37.72 − 0.01756Y ear
a. Computer output gives the fitted regression model as W idth
b. As Year increases by 1, Width decreases by 0.01756 mm, on average.
c. Plugging 1966 into the fitted regression equation, we get 37.72 − 0.01756(1966) = 3.197 mm.
1.16 ˆ = −8.98 + 7.33Lantern.
a. The computer output gives the fitted regression model as Eggs
b. As lantern size increases by 1 mm, the predicted number of eggs laid increases by 7.3 on
average.
c. Plugging 14 into the fitted regression equation, we get −8.98 + 7.33(14) = 93.6 eggs.
1.17 a. The computer output gives the fitted regression equation as M axGrip̂S trength =
36.16 + 4.705Attractive.
b. As Attractive increases by 1, MaxGripStrength increases by 4.7 kg, on average.
c. Plugging 3 into the fitted equation from part (a) we get a predicted M axGrip̂S trength =
36.16 + 4.705(3) = 50.3 kg.
1.18 a. The computer output gives the fitted regression equation as M axGrip̂S trength = 9.3 +
29.0SHR.
b. As SHR increases by 1, MaxGripStrength increases by 29 kg, on average.
c. Plugging 1.5 into the fitted equation from part (a) we get a predicted M axGrip̂S trength =
9.3 + 29.0(1.5) = 52.8 kg.
1.19 a. The scatterplot shows a moderate positive association between Calories and Sugar.
, Chapter 1 1-3
160
140
120
Calories
100
80
60
0 5 10 15
Sugar
b. Based on regression output, the prediction equation is Cal
lories = 87.43 + 2.48Sugar.
c. For every additional gram of sugar in a serving of cereal, the expected calories increase by
2.48 calories.
1.20 a. There is a clear, linear, and strong relationship between list price and sale price, as the
plot indicates.
4e+05
SalePrice
0e+00
0e+00 2e+05 4e+05 6e+05
ListPrice
b. The regression summary is given below.
SOLUTION MANUAL
,Chapter 1 1-1
Chapter 1 Solutions
1.1 Part (c) is false. The predicted value of Y when X = 2 is Ŷ = 100 + 15(2) = 130, not 110.
Parts (a), (b), and (d) are true.
1.2 A residual plot does not help assess (c) the condition of independence of the residuals. It does
help assess (a) linearity, (b) constant variance, and (d) zero mean.
1.3 The slope is given in the output under the heading Coef for the predictor W ingLength. The
estimate is β̂1 = 0.4674.
1.4 The slope is given in the output under the heading Coef for the predictor Y ear. The estimate
is β̂1 = 0.01251.
1.5 The intercept is given in the output under the heading Coef for the Constant. The estimate
is β̂0 = 1.3655.
1.6 The intercept is given in the output under the heading Coef for the Constant. The estimate
is β̂0 = −16.47.
1.7 As wing length increases by 1 mm, the weight increases by 0.4674 g, on average.
1.8 As year increases by 1, the length of the winning long jump increases by 0.01251 m, on average.
1.9 The regression standard error is given in the output as S = 1.39959. We can also compute
this from the information given in the Error row of the Analysis of Variance:
SSE 223.31 √
σˆE = = = 1.959 = 1.39959
n−2 116 − 2
A typical deviation of a sparrow weight from the line predicted by its wing length might be about
1.4 grams.
1.10 The regression standard error is given in the output as S = 0.259522. We can also compute
this from the information given in the Error row of the Analysis of Variance:
SSE 1.751 √
σˆE = = = 0.06735 = 0.2595
n−2 28 − 2
A typical deviation of a winning Olympic long jump length from the line predicted by its year
might be about 0.26 meters.
1.11 The degrees of freedom for the regression standard error are n − 2 = 116 − 2 = 114. The
value also appears in the DF column of the Analysis of Variance section of the output.
,1-2 Chapter 1
1.12 The degrees of freedom for the regression standard error are n − 2 = 28 − 2 = 26. The value
also appears in the DF column of the Analysis of Variance section of the output.
1.13 The predicted value is ŷ1 = 25 + 7(10) = 95. The residual is y1 − ŷ1 = 100 − 95 = 5.
1.14 The predicted value is ŷ1 = 78 − 0.5(30) = 63. The residual is y1 − ŷ1 = 60 − 63 = −3.
1.15 ˆ = 37.72 − 0.01756Y ear
a. Computer output gives the fitted regression model as W idth
b. As Year increases by 1, Width decreases by 0.01756 mm, on average.
c. Plugging 1966 into the fitted regression equation, we get 37.72 − 0.01756(1966) = 3.197 mm.
1.16 ˆ = −8.98 + 7.33Lantern.
a. The computer output gives the fitted regression model as Eggs
b. As lantern size increases by 1 mm, the predicted number of eggs laid increases by 7.3 on
average.
c. Plugging 14 into the fitted regression equation, we get −8.98 + 7.33(14) = 93.6 eggs.
1.17 a. The computer output gives the fitted regression equation as M axGrip̂S trength =
36.16 + 4.705Attractive.
b. As Attractive increases by 1, MaxGripStrength increases by 4.7 kg, on average.
c. Plugging 3 into the fitted equation from part (a) we get a predicted M axGrip̂S trength =
36.16 + 4.705(3) = 50.3 kg.
1.18 a. The computer output gives the fitted regression equation as M axGrip̂S trength = 9.3 +
29.0SHR.
b. As SHR increases by 1, MaxGripStrength increases by 29 kg, on average.
c. Plugging 1.5 into the fitted equation from part (a) we get a predicted M axGrip̂S trength =
9.3 + 29.0(1.5) = 52.8 kg.
1.19 a. The scatterplot shows a moderate positive association between Calories and Sugar.
, Chapter 1 1-3
160
140
120
Calories
100
80
60
0 5 10 15
Sugar
b. Based on regression output, the prediction equation is Cal
lories = 87.43 + 2.48Sugar.
c. For every additional gram of sugar in a serving of cereal, the expected calories increase by
2.48 calories.
1.20 a. There is a clear, linear, and strong relationship between list price and sale price, as the
plot indicates.
4e+05
SalePrice
0e+00
0e+00 2e+05 4e+05 6e+05
ListPrice
b. The regression summary is given below.