Infinite Limits
There are 2 types of limits that involve infinity that come up frequently.
1. An Infinite Limit- The value of a function increases or decreases without
bound as 𝑥 approaches a finite point 𝑎 .
2. Limit at Infinity- finding a limit when 𝑥 (or the independent variable)
increases or decreases without bound (discussed in the next section)
1
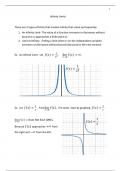
Ex. An Infinite Limit. Let 𝑓 (𝑥 ) = . lim 𝑓 (𝑥 ) = ∞.
𝑥2 𝑥→0
1
𝑓 (𝑥 ) =
𝑥2
1 1
Ex. Let 𝑓 (𝑥 ) = , Find lim 𝑓 (𝑥 ), if it exists. Start by graphing 𝑓 (𝑥 ) = .
𝑥 𝑥→0 𝑥
lim 𝑓(𝑥) = Does Not Exist (DNE), 1
𝑥→0 𝑓 (𝑥 ) =
𝑥
Because 𝑓(𝑥) approaches +∞ from
the right and −∞ from the left.
, 2
Def. Suppose 𝑓(𝑥) is defined for all 𝑥 near 𝑥 = 𝑎. If 𝑓(𝑥) grows arbitrarily
large for all 𝑥 sufficiently close (but not equal) to 𝑎 , we write 𝐥𝐢𝐦 𝒇(𝒙) = ∞
𝒙→𝒂
and say that the limit of 𝑓(𝑥) as 𝑥 approaches a is infinity.
𝑦 = 𝑓(𝑥)
𝑥=𝑎
If 𝑓(𝑥) is negative and grows arbitrarily large in magnitude for all 𝑥 sufficiently
close (but not equal) to 𝑎 , we write 𝐥𝐢𝐦 𝒇(𝒙) = −∞ and say that the limit of
𝒙→𝒂
𝑓(𝑥) as 𝑥 approaches 𝑎 is negative infinity.
𝑥=𝑎
𝑦 = 𝑓(𝑥)