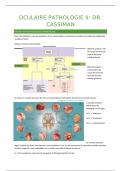
Enkelvoudige lineaire regressie
We fitten een lijn op basis van 2 continue variabelen (covariaten) → 𝑌 = 𝛽0 + 𝛽1 ∗ 𝑋
Hypotheses:
• Intercept
o H0 : β0 =0
Indien β1 =0 , betekent dit ook dat R2 = 0 en dat ρ2 =0
• Richtingscoefficient
o H0 : β1 =0 Enkelvoudige lineaire regressie heeft maar 1 dummy variabele → > 1 degrees
• Populatievariantie of freedom is nooit een enkelvoudige lineaire regressie tabel
o H0 : ρ2 =0
Formules:
𝑆𝑆𝑅 𝑆𝑆𝑏𝑒𝑡𝑤𝑒𝑒𝑛 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑒 𝑣𝑒𝑟𝑘𝑙𝑎𝑎𝑟𝑑 𝑑𝑜𝑜𝑟 𝑥
• 𝑅2 = = =
𝑆𝑆𝑇𝑂 𝑆𝑆𝑇𝑂 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑒 𝑧𝑜𝑛𝑑𝑒𝑟 𝑥 𝑖𝑛 𝑟𝑒𝑘𝑒𝑛𝑖𝑛𝑔 𝑡𝑒 𝑏𝑟𝑒𝑛𝑔𝑒𝑛
• Pearson correlatie (r) = ± √𝑅 2 (het teken van β1 = het teken van correlatie)
𝑆𝑆𝑚𝑜𝑑𝑒𝑙/(𝑟−1) 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑒 𝑣𝑒𝑟𝑘𝑙𝑎𝑎𝑟𝑑 𝑑𝑜𝑜𝑟 𝑥
• 𝐹 = 𝑆𝑆𝑟𝑒𝑠𝑖𝑑𝑢𝑎𝑙/(𝑁−𝑟)
= 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑒 𝑑𝑖𝑒 𝑛𝑖𝑒𝑡 𝑣𝑒𝑟𝑘𝑙𝑎𝑎𝑟𝑑 𝑤𝑜𝑟𝑑𝑡 𝑑𝑜𝑜𝑟 𝑥
• 𝛽0 = 𝑌 - 𝛽1 ∗ 𝑋 (indien snijpunt niet zichtbaar op figuur)
Eerst zonder x, dan met x (er blijft nog variatie over)
Stappenplan:
• Kijk naar de assen
o Klein naar groot of omgekeerd?
o Zelfde schaal op beide figuren?
• Is het snijpunt (x=0) zichtbaar op de grafiek?
o Neen → bereken rico en zo het snijpunt (𝛽0 = 𝑌 - 𝛽1 ∗ 𝑋)
,Meervoudige lineaire regressie
We fitten een vlak op basis van > 2 continue variabelen (covariaten), er moet ook
nagegaan worden of er een interactie is tussen de predictors. → Yi = β0 + β1Xi1 + β2Xi2
Zelfde hypotheses als enkelvoudige, maar voor alle β -waarden
Formules:
𝑆𝑆𝑅 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑒 𝑣𝑒𝑟𝑘𝑙𝑎𝑎𝑟𝑑 𝑑𝑜𝑜𝑟 𝑥
• 𝑅 2 = 𝑆𝑆𝑇𝑂 = 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑒 𝑧𝑜𝑛𝑑𝑒𝑟 𝑥 𝑖𝑛 𝑟𝑒𝑘𝑒𝑛𝑖𝑛𝑔 𝑡𝑒 𝑏𝑟𝑒𝑛𝑔𝑒𝑛
o Veel factoren → meer kans op kleinere R2 door toeval →
adjusted R2
𝑆𝑆𝑚𝑜𝑑𝑒𝑙/(𝑟−1) 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑒 𝑣𝑒𝑟𝑘𝑙𝑎𝑎𝑟𝑑 𝑑𝑜𝑜𝑟 𝑥
• 𝐹 = =
𝑆𝑆𝑟𝑒𝑠𝑖𝑑𝑢𝑎𝑙/(𝑁−𝑟) 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑒 𝑑𝑖𝑒 𝑛𝑖𝑒𝑡 𝑣𝑒𝑟𝑘𝑙𝑎𝑎𝑟𝑑 𝑤𝑜𝑟𝑑𝑡 𝑑𝑜𝑜𝑟 𝑥
We kunnen het meervoudige model ook vergelijken met het enkelvoudige model door ‘x’ als het
meervoudig model te beschouwen.
Interpretatie:
• Enkelvoudige uitspraken over of X2 significante extra informatie geeft bovenop X1
o Bv. na correctie voor X2 is er geen/wel significant verband gevonden tussen X1 en Y
o Niet: er is geen significant verband tussen Y en X1 en X2
Stappenplan:
• Is het snijpunt zichtbaar op de figuur (of kan je het berekenen)?
• Kijk naar de assen → klein naar groot of omgekeerd?
• Stijgt Y wanneer X1 stijgt bij een vaste waarde voor X2?
• Stijgt Y wanneer X2 stijgt bij een vaste waarde voor X1?
• Interactie
o Wordt de positieve/negatieve helling kleiner/groter naargelang X1 stijgt? (onderkant
en bovenkant van vlak vergelijken)
▪ Ja, de negatieve helling wordt kleiner (en dus positiever) → kwadratisch
verband is positief
▪ Neen, de negatieve helling wordt groter (en dus negatiever) → kwadratisch
verband is negatief
▪ Kan ook door te herleiden naar wat rico van de dosis is (vaste waarde X1) en
verschillende waarden in te vullen → kijken of helling positiever/negatiever
wordt
• 𝛽0 = 8,91 + 0,06𝑥2
• 𝛽1 = (0,014𝑥2 − 0,46)
• 𝛽1 = (0,014 ∗ 20 − 0,46) = −0,18
• 𝛽1 = (0,014 ∗ 30 − 0,46) = −0,04
,ANOVA
We plotten een relatie tussen een onafhankelijke categorische (factor, minstens 3 groepen) en een
afhankelijke continue variabele. We weten enkel of de groepen verschillen, niet op welke manier of
welke groepen. ANOVA vermijdt het multiple testing probleem van meerdere t-testen. Een
significant ANOVA-test betekent niet automatisch dat een van de t-testen significant zou zijn want
de t-test heeft lagere power.
Hypothese:
• H0 :µ1= µ2= µ3 =µ4
ANOVA hypothese A is significant (ANOVA gezien in een MANOVA)
Formules:
𝑆𝑆𝑅 𝑆𝑆𝑏𝑒𝑡𝑤𝑒𝑒𝑛 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑒 𝑣𝑒𝑟𝑘𝑙𝑎𝑎𝑟𝑑 𝑑𝑜𝑜𝑟 𝑥
• 𝑅 2 = 𝑆𝑆𝑇𝑂 = 𝑆𝑆𝑇𝑂
= 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑒 𝑧𝑜𝑛𝑑𝑒𝑟 𝑥 𝑖𝑛 𝑟𝑒𝑘𝑒𝑛𝑖𝑛𝑔 𝑡𝑒 𝑏𝑟𝑒𝑛𝑔𝑒𝑛
𝑀𝑆𝐶 𝑆𝑆𝑚𝑜𝑑𝑒𝑙/(𝑟−1) 𝑆𝑆𝑏𝑒𝑡𝑤𝑒𝑒𝑛/(𝑟−1) 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑒 𝑣𝑒𝑟𝑘𝑙𝑎𝑎𝑟𝑑 𝑑𝑜𝑜𝑟 𝑥
• 𝐹 = 𝑀𝑆𝐸 = 𝑆𝑆𝑟𝑒𝑠𝑖𝑑𝑢𝑎𝑙/(𝑁−𝑟)
= 𝑆𝑆𝑤𝑖𝑡ℎ𝑖𝑛/(𝑁−𝑟) = 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑒 𝑑𝑖𝑒 𝑛𝑖𝑒𝑡 𝑣𝑒𝑟𝑘𝑙𝑎𝑎𝑟𝑑 𝑤𝑜𝑟𝑑𝑡 𝑑𝑜𝑜𝑟 𝑥
GLM:
• Hypothese test of ricos 0 zijn → = testen of gemiddelden gelijk zijn
• De referentiegroep veranderen heeft enkel effect op interpretatie, niet op p-waarden
• #dummy variabelen = # vrijheidsgraden
• Voorbeeld: factor met 4 niveaus/groepen → 3 dummy variabelen nodig → 3 vrijheidsgraden
Stappenplan:
• Is de variabiliteit gelijk in beide figuren?
o Wat is de SSbetween? Zijn de gemiddeldes hetzelfde op beide figuren?
o Verschilt de totale variabiliteit? Is er meer variabiliteit binnen de groepen op een
figuur?
o Bereken R2 = SSbetween/SStotaal (groter is beter)
,MANOVA
We plotten een relatie tussen meerdere onafhankelijke categorische (factoren, minstens 3
groepen) en afhankelijke continue variabelen. Er moet ook nagegaan worden of er een interactie is
tussen de predictors. MANOVA heeft meer power dan ANOVA, er kunnen dus significante relaties
gevonden worden in MANOVA terwijl deze niet significant waren in ANOVA ookal is het effect even
groot.
Hypothese:
• H0 :µ1= µ2= µ3 =µ4
o Zijn de gemiddelden voor alle niveaus van x1 gelijk? (gemiddelden van beide hele
kolommen)
o Zijn de gemiddelden voor alle niveaus van x2 gelijk? (gemiddelden links-links
vergelijken met gemiddelden van rechts-rechts)
o Is er interactie tussen x1 en x2? (enkel indien interactie is toegelaten)
Behandeling A is significant Behandeling B is significant Geen interactie
Formules:
𝑆𝑆𝑅 𝑆𝑆𝑏𝑒𝑡𝑤𝑒𝑒𝑛 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑒 𝑣𝑒𝑟𝑘𝑙𝑎𝑎𝑟𝑑 𝑑𝑜𝑜𝑟 𝑥
• 𝑅 2 = 𝑆𝑆𝑇𝑂 = 𝑆𝑆𝑇𝑂
= 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑒 𝑧𝑜𝑛𝑑𝑒𝑟 𝑥 𝑖𝑛 𝑟𝑒𝑘𝑒𝑛𝑖𝑛𝑔 𝑡𝑒 𝑏𝑟𝑒𝑛𝑔𝑒𝑛
𝑀𝑆𝐶 𝑆𝑆𝑚𝑜𝑑𝑒𝑙/(𝑟−1) 𝑆𝑆𝑏𝑒𝑡𝑤𝑒𝑒𝑛/(𝑟−1) 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑒 𝑣𝑒𝑟𝑘𝑙𝑎𝑎𝑟𝑑 𝑑𝑜𝑜𝑟 𝑥
• 𝐹 = 𝑀𝑆𝐸 = 𝑆𝑆𝑟𝑒𝑠𝑖𝑑𝑢𝑎𝑙/(𝑁−𝑟)
= 𝑆𝑆𝑤𝑖𝑡ℎ𝑖𝑛/(𝑁−𝑟) = 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑒 𝑑𝑖𝑒 𝑛𝑖𝑒𝑡 𝑣𝑒𝑟𝑘𝑙𝑎𝑎𝑟𝑑 𝑤𝑜𝑟𝑑𝑡 𝑑𝑜𝑜𝑟 𝑥
Interactie:
• Geen → som van de effecten = som van de individuele effecten → additief
• Wel → som van de effecten ≠ som van de individuele effecten → niet additief
• Grafische voorstelling interactie:
o Trek een lijn door elk niveau van een factor en herhaal dit voor de andere factoren
o Lijnen kruisen = (significante) interactie
o Als de lijnen kruisen en de interactie niet significant is, is dit gelijk aan parallelle
lijnen
, ANCOVA
We plotten een relatie tussen een continue respons en meerdere onafhankelijke categorische
(factoren, minstens 3 groepen) en continue variabelen (covariaten, zijn onafhankelijk , kunnen niet
gerandomiseerd worden en verklaren ook een deel van de variabiliteit). Het model corrigeert voor
verschillen die niet gerandomiseerd konden worden en verandert de posities van de gemiddelden
voor het geval dat alle proefpersonen dezelfde waarden hadden voor de covariaat.
➔ kleinere SSE (= SSwithin = SSresidual) → MSE kleiner → meer power voor F-test
ANCOVA is an extension of ANOVA in which main effects and interactions are assessed after
dependent variable scores are adjusted for differences associated with one or more covariates
that are measured before the dependent variable and are correlated with it.
Formules:
𝑆𝑆𝑅 𝑆𝑆𝑏𝑒𝑡𝑤𝑒𝑒𝑛 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑒 𝑣𝑒𝑟𝑘𝑙𝑎𝑎𝑟𝑑 𝑑𝑜𝑜𝑟 𝑥
• 𝑅2 = = =
𝑆𝑆𝑇𝑂 𝑆𝑆𝑇𝑂 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑒 𝑧𝑜𝑛𝑑𝑒𝑟 𝑥 𝑖𝑛 𝑟𝑒𝑘𝑒𝑛𝑖𝑛𝑔 𝑡𝑒 𝑏𝑟𝑒𝑛𝑔𝑒𝑛
𝑀𝑆𝐶 𝑆𝑆𝑚𝑜𝑑𝑒𝑙/(𝑟−1) 𝑆𝑆𝑏𝑒𝑡𝑤𝑒𝑒𝑛/(𝑟−1) 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑒 𝑣𝑒𝑟𝑘𝑙𝑎𝑎𝑟𝑑 𝑑𝑜𝑜𝑟 𝑥
• 𝐹 = = = =
𝑀𝑆𝐸 𝑆𝑆𝑟𝑒𝑠𝑖𝑑𝑢𝑎𝑙/(𝑁−𝑟) 𝑆𝑆𝑤𝑖𝑡ℎ𝑖𝑛/(𝑁−𝑟) 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑒 𝑑𝑖𝑒 𝑛𝑖𝑒𝑡 𝑣𝑒𝑟𝑘𝑙𝑎𝑎𝑟𝑑 𝑤𝑜𝑟𝑑𝑡 𝑑𝑜𝑜𝑟 𝑥
Grafisch:
• Covariaat heeft geen effect → lijnen op scatterplot horizontaal (eigenlijk zelfde als ANOVA)
• Covariaat heeft effect → helling
• Covariaat verklaart alles (groepen geen effect) → rechten in elkaars verlengde
• Lijnen hebben verschillende hellingen (kruisen) → interactie
Covariaat verklaart niets covariaat verklaart variatie deels covariaat verklaart alles interactie
GLM-notatie: