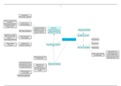
EIN-GRUPPEN T-TEST
(1) Null- und Alternativhypothese
(2) Berechnung des Mittelwerts xquer, Schätzer für Populationsstreuung sigma dach von x
und Standardfehler sigma dach von xquer
(3) Berechnung des empirischen t-Werts !
”wie viele Standardfehler liegt der Mittelwert von der Konstanten entfernt?”
(4) Vergleich mit kritischem t-Wert !*+,-(8 − 1; ;)
(5) Interpretation und Entscheidung für H0 oder H1
Regression:
Prädiktor X
Kriterium Y
Regressionsgerade YDach i=b*xi+a
Intercept=Regressionskonstante ay,x
Regressionsgewicht=Steigung by,x
Vorhersage YDachi
Residuum=Vorhersagefehler, Abstand zwischen Schätzer YDachi und tatsächlichem Wert Yi
Residualvarianz=Varianz der Residuen
Methode der kleinsten Quadrate
Vorteile:
(1) Eliminierung negativer Vorzeichen
(2) Stärkere Abweichungen werden mehr berücksichtigt à besserer fit
Standarschätzfehler der Regression:
Populationsschätzer des Standardschätzfehlers:
SStotal=SSbetween+SSwithin
Yij(einzelner Messwert)=Yquer(Gesamtmittelwert)+aj(Effekt:erklärbar)+eij(Fehler: nicht erklärbar)
eij=yij - yquer
Berechnung ANOVA
1. Hypothesen H0 und H1
2. Berechnung der unstandardisierten Quadratsummen SStotal, SSwithin, SSbetween
3. Berechnung der Freiheitsgrade dftotal, dfwithin, dfbetween
4. Berechnung der mittleren Quadratsummen MStotal, MSwithin, MSbetween
5. Berechnung des empirischen F-Werts Femp
6. Vergleich von Fkrit und Femp
7. Entscheidung für H0 oder H1
Voraussetzungen einfaktorielle Varianzanalyse (ANOVA)
• Nominalskalierte UV
• Intervallskalierte AV
• Normalverteile AV. Prüfung über Kolmogorov-Smirnov-Test H0: ”Die Variable ist normalverteilt”
(1) Null- und Alternativhypothese
(2) Berechnung des Mittelwerts xquer, Schätzer für Populationsstreuung sigma dach von x
und Standardfehler sigma dach von xquer
(3) Berechnung des empirischen t-Werts !
”wie viele Standardfehler liegt der Mittelwert von der Konstanten entfernt?”
(4) Vergleich mit kritischem t-Wert !*+,-(8 − 1; ;)
(5) Interpretation und Entscheidung für H0 oder H1
Regression:
Prädiktor X
Kriterium Y
Regressionsgerade YDach i=b*xi+a
Intercept=Regressionskonstante ay,x
Regressionsgewicht=Steigung by,x
Vorhersage YDachi
Residuum=Vorhersagefehler, Abstand zwischen Schätzer YDachi und tatsächlichem Wert Yi
Residualvarianz=Varianz der Residuen
Methode der kleinsten Quadrate
Vorteile:
(1) Eliminierung negativer Vorzeichen
(2) Stärkere Abweichungen werden mehr berücksichtigt à besserer fit
Standarschätzfehler der Regression:
Populationsschätzer des Standardschätzfehlers:
SStotal=SSbetween+SSwithin
Yij(einzelner Messwert)=Yquer(Gesamtmittelwert)+aj(Effekt:erklärbar)+eij(Fehler: nicht erklärbar)
eij=yij - yquer
Berechnung ANOVA
1. Hypothesen H0 und H1
2. Berechnung der unstandardisierten Quadratsummen SStotal, SSwithin, SSbetween
3. Berechnung der Freiheitsgrade dftotal, dfwithin, dfbetween
4. Berechnung der mittleren Quadratsummen MStotal, MSwithin, MSbetween
5. Berechnung des empirischen F-Werts Femp
6. Vergleich von Fkrit und Femp
7. Entscheidung für H0 oder H1
Voraussetzungen einfaktorielle Varianzanalyse (ANOVA)
• Nominalskalierte UV
• Intervallskalierte AV
• Normalverteile AV. Prüfung über Kolmogorov-Smirnov-Test H0: ”Die Variable ist normalverteilt”