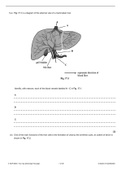
TriaIdentifies
Double As a
of Inverse Trig functions
- -
tan-si * [Sint 7 Fu u
cos(26) = cost -
sin6 *(csu) :22.
- I
1- x
2 tanf
cot == En tan (28) Franco
=
* [tan"u] it =
I
[esn] :
r
since
u2 -1
sin cos
S
I
ese = see -
,
2
Sin'Escos 8 = / tan() =
M
·
1 - cos' 8
#Eric
Frig Functions
-
Sin 8 =
.
(25] x
sinto- Hes
-
e
coso = 1 - Since 2
Sinhx = -
2
es(20)
+
i
coso-
2 2
(20)
tan 8 s 1 = See 8 tano-I-cos
& (20) - cos
tanto-sees-I
see'D-tano = I
Integration
Frigonometric Table
Ssinxdx = - cesX + c
cott) =
cs28
ScosXdx = sinx o
cot20 = eso-I Stanx dx In/seex) = b Trig Identities
Hyperic
(scO-coto =
/ Sseaxtanx seex = + ↳ sinh(-x) = -
sinh x
Scsexcotx dx = -
cex + >
-
cosh)-x) =
cosh x
!
sin(-0) -Sind dx
see'x tanx coshix-sintix /
=
>
c
-
= + =
cs)-0) -esO =
usex dx = cotX +c >
-
sinh(x +y) Sinhxcoshyo coshxsinhy =
! lu/cx-cotxloc
tan(- f) tanf dx cosh(X x)
esex
>
coshxceshy sinkxsinhy
-
= = -
=
+ a
cot) 8) = -
co to see dx In/seax tanx/oa
x =
o
>
-
Sinh2x = 2 sinhxcoshx
cos)- 8) : cost Scotxdx lu/sin x loc = >
-
cosh2x = cash2X o Sinhix
see( 8) - = Seco >
-
coshix =
&(1 cosh2x) +
use
Try functions - >
sinhix = (1 cosh2x) +
( 1]
&
Sum : Difference
-
Formulas sin(sinix) = x +
1
,
( 1)
-
cos(X +
B) =
costcosB-sin Sin cos(cos"x) = X -
1
, Calculus
of HyperteTrigeunctions
cos (X-B) :
costcosBe sind sink tan(tanix) =
x [-x x] , [sinhu) coshu * =
I
Sin (B) =
Sinsing -
s Xest sin"(sinx) = X [E ,& * [coshu] = Sinhu d -
X
sin(X-B) =
SindsinB a cosX cost cos" (losx) = X [0 i] , [tanhu] =
sechtn .
tan" (tanx) = X
( -
[eschu] = - eschu ethu . 7
tan
tan(x-B) eas es(csix) * [sech u] sechutanhu .
-
= X =
tanxtau
-
=
[cothu) eschin E
-
see(sex) = X = -
·
tanx-tan
,
tan(X-B) =
ct(ct"x) x
coshu du sinhu
T
tano
=
& tanB
=
+
csi'(cxx) = x
sinhu du = coshu + a
see"(secx) = x sech'u du = tanhu x
cot (c+ x) = X
eschu cothu ·
du = -eschus a
sechn tanhu . du = -Sechu oc
eschiu du =
-cothu -c