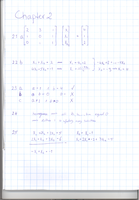Summary Reference Notes for Final Exam

VA bottom of
Asymptotes : Vertical : in the a rational function

Holes : Holes form
by canceling a Vertical Asymptote in the bottom

Horizontal : HA :DegreeA_ A CB , the HA is y= 0


A to find
Degree B > B , there is no HA .
Use
polynomial division
its slant asymptote .




A :B divide the leading coefficients
conics


Finding p in a parabolic equation YZ=4px rewrite the number as 4. p




<
2
Distance formula D= ( Xz (y y 1)
✗
1) +
-
-



,



Exponential & Logarithmic Functions

The domain of a log function is Hue
range
of an exponential function .




Exponants Inverse
property logbc __ a ba=c


One to - -
One
property b "=bW it u=w
1. Isolate the exponential
function
"+W=
"

Product rule f- lutw )= f- (a) f- ( w ) so b b + bw -


Try to make the bases =


exponents
then equate the



flu )=¥÷
"
W= b÷w If that doesn't work take
-

-




Quotient rule b
,
-
w so
the 1h of both sides

& use the power


(flu ) )W= (b )W= " W

f- (
" rule
Power rule UW ) so b


1. Isolate the logarithmic
Logs function.
Product rule
logbluw )= logblu ) + logblw ) 2. (a) If convenient, express
both sides as logs with the
same base and equate the
Quotient rule
1ogb(%)= logblu )
-




logblwl arguments
of the log functions.
(b) Otherwise, rewrite the
Power rule
logbluw)= Wlogblul log equation as an
exponential equation.
of base formula
Change change to based :
logba =
10yd (a)
b)
log , /
h k h±k

ogxb
' "

Log tricks :
logbx ± logbx =
logbx so
logx +
log ✗ =/




{
( htk )


{
Distributing logbx =
hlogbxtklogbx note the difference between

these rules !

multiplying arguments logbhk =
logbh +
logbk

Dealing with roots
109b¥ =
109b¥ ntlogbx =