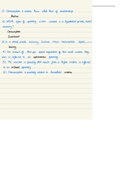
Conjugate And Modulus
In the previous section we looked at algebraic operations on complex numbers.Th
other operations that we should take a look at since they tend to show up on occa
a look at quite a few nice facts about these operations.
Complex Conjugate
The first one we’ll look at is the complex conjugate, (or just the conjugate).Given
number z = a + bi the complex conjugate is denoted by ¯z̄¯ and is defined to be,
¯z̄
¯ = a − bi
In other words, we just switch the sign on the imaginary part of the number.
Here are some basic facts about conjugates.
¯¯¯
¯z̄
¯ =z
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
z1 ± z2 = ¯z̄¯ 1 ± ¯z̄¯ 2
¯z¯¯¯¯¯z
1 2
¯¯¯ = ¯z̄¯ 1 ¯z̄¯ 2
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ ¯z̄
¯
z1
( )=
1
z2 ¯z̄
¯
2
The first one just says that if we conjugate twice we get back to what we started w
hopefully this makes some sense.The remaining three just say we can break up s
products and quotients into the individual pieces and then conjugate.
So, just so we can say that we worked a number example or two let’s do a couple
illustrating the above facts.
Example 1 Compute each of the following.
¯¯¯
(a) ¯z̄¯ for z = 3 − 15i
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
(b) z1 − z2 for z1 = 5 + i and z2 = −8 + 3i
(c) ¯z¯¯¯1¯ − ¯z¯¯¯2¯ for z1 = 5 + i and z2 = −8 + 3i
Hide Solution !
There really isn’t much to do with these other than to so the work so,
In the previous section we looked at algebraic operations on complex numbers.Th
other operations that we should take a look at since they tend to show up on occa
a look at quite a few nice facts about these operations.
Complex Conjugate
The first one we’ll look at is the complex conjugate, (or just the conjugate).Given
number z = a + bi the complex conjugate is denoted by ¯z̄¯ and is defined to be,
¯z̄
¯ = a − bi
In other words, we just switch the sign on the imaginary part of the number.
Here are some basic facts about conjugates.
¯¯¯
¯z̄
¯ =z
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
z1 ± z2 = ¯z̄¯ 1 ± ¯z̄¯ 2
¯z¯¯¯¯¯z
1 2
¯¯¯ = ¯z̄¯ 1 ¯z̄¯ 2
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ ¯z̄
¯
z1
( )=
1
z2 ¯z̄
¯
2
The first one just says that if we conjugate twice we get back to what we started w
hopefully this makes some sense.The remaining three just say we can break up s
products and quotients into the individual pieces and then conjugate.
So, just so we can say that we worked a number example or two let’s do a couple
illustrating the above facts.
Example 1 Compute each of the following.
¯¯¯
(a) ¯z̄¯ for z = 3 − 15i
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
(b) z1 − z2 for z1 = 5 + i and z2 = −8 + 3i
(c) ¯z¯¯¯1¯ − ¯z¯¯¯2¯ for z1 = 5 + i and z2 = −8 + 3i
Hide Solution !
There really isn’t much to do with these other than to so the work so,