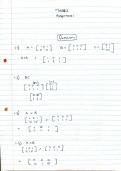1CV00 – fundamentals of
operations management
Week 1:
Linear programming:
MAX (or MIN): f 0 (X 1 , X 2 , … , X n )
Constraints: f 1 ( X 1 , X 2 , … , X n ) ≤b 1
f k ( X 1 , X 2 , … , X n ) ≥b k
f m ( X 1 , X 2 , … , X n )=bm
Plot the constraints, optimal solution occurs where constraints intersect.
Inventory control:
Relevant costs:
Holding costs
Order and production costs
Shortage costs
Details on relevant costs:
Order costs = average number of order per time unit * costs per order
Purchasing costs = average number of orders per time unit * number of products
bought per order * cost per unit of product
Holding costs = average number of products on stock * holding costs per product per
time unit
Costs per cycle:
h∗Q
∗Q
2
K +cQ+
D
One fixed order cost (K)
Buy Q products (cQ)
Average inventory (Q/2)
Cycle duration (Q/D)
,Costs per year:
( )
h∗Q
∗Q
D 2 K∗D h∗Q
G ( Q )= ∗ K + cQ+ = + cD+
Q D Q 2
Demand D
D/Q orders
Average inventory Q/2
Optimal order quantity: Q¿ =±
√ 2 KD
h
Optimal order quantity when shortages are allowed: Q¿ =
√ 2 KD ( h+ s )
sh
Lagrange approach when multiple products have to fit in one warehouse: Q i =
¿
√ 2 K i Di
hi +2 θ c i
with θ (>0) such that the total capacity fits exactly: ∑ ci Qi=C
i
n
If the constraint is active: Q =m EOQ i where m=C / ∑ ( c i EOQi )
¿
i=1
Optimal annual costs: G ( Q )= √ 2 hKD +cD
¿
Production with finite production rate P:
D 1Q Q
Annual costs: G ( Q )= ( K + cQ+h ( P−D ) ), where D/Q is # cycles, cQ is production
Q 2P D
costs, h*1/2 is holding costs, Q/P(P-D) is maximum inventory and Q/D is cycle length.
Optimal size production run: Q=
√ 2 KD
h '
' D
where h =h(1− ) and P> D
P
Annual holding and set-up costs: √ 2 KDh '
Ordering multiple products: same cycle
2
T T
Costs per cycle:C ( T )= A+ ∑ (¿ a i+ hi Qi )=A + ∑ ( ai +hi D i )¿
i 2 i 2
A+ ∑ ai
Costs per time unit: C ( T ) = i
+ ∑ hi D i
T
T T i 2
Minimum costs at: T =√ 2 ¿¿ ¿
, Ordering multiple products: different cycles
Suppose product i is ordered every mi cycles:
Minimum costs are achieved at: T =√ 2 ¿¿ ¿
Week 2:
Lot sizing
In periodic lot sizing we consider the problem that a supplier meets in situations where
demand for products is not simply delivered from stock, but where some processing steps
have to be done before the shipment. Demand is fully known for a number of periods, the
so-called horizon, and no information is available for periods after the horizon. Two types of
costs are balanced: production set-up costs and the inventory holding costs.
Definitions and standard assumptions:
Y(t) = inventory position at the end of period t
D(t) = total demand in period t
Q(t) = production order quantity in period t
H = the number of known demand periods (horizon)
A = the fixed setup or replenishment costs
h = the carrying costs per unit of inventory per period
Rules based upon average demand
If the average demand level is D per period, the quantity is given by: EOQ = √ (¿ 2 AD /h) ¿
Rule 1: fixed quantity EOQ rule
We first determine the EOQ quantity, usually with the D-level based upon the average
demand during H periods of known demand. This quantity is rounded to the nearest integer
Qf.
Rule 2: EOQ rule
We first determine the EOQ quantity, usually with the D-level based upon the average
demand during H periods of known demand. Now, every time we produce, we will try to get
as close as possible to this quantity.
Rule 3: TEOQ fixed cycle rule (POQ)
We first determine the EOQ quantity, usually with the D-level based upon the average
demand during H periods of known demand. When we divide the EOQ quantity by the
average demand, we obtain the average time between two replenishments TEOQ. This is
rounded to the nearest integer. Every time we produce, we produce the demand for this
number of periods.
operations management
Week 1:
Linear programming:
MAX (or MIN): f 0 (X 1 , X 2 , … , X n )
Constraints: f 1 ( X 1 , X 2 , … , X n ) ≤b 1
f k ( X 1 , X 2 , … , X n ) ≥b k
f m ( X 1 , X 2 , … , X n )=bm
Plot the constraints, optimal solution occurs where constraints intersect.
Inventory control:
Relevant costs:
Holding costs
Order and production costs
Shortage costs
Details on relevant costs:
Order costs = average number of order per time unit * costs per order
Purchasing costs = average number of orders per time unit * number of products
bought per order * cost per unit of product
Holding costs = average number of products on stock * holding costs per product per
time unit
Costs per cycle:
h∗Q
∗Q
2
K +cQ+
D
One fixed order cost (K)
Buy Q products (cQ)
Average inventory (Q/2)
Cycle duration (Q/D)
,Costs per year:
( )
h∗Q
∗Q
D 2 K∗D h∗Q
G ( Q )= ∗ K + cQ+ = + cD+
Q D Q 2
Demand D
D/Q orders
Average inventory Q/2
Optimal order quantity: Q¿ =±
√ 2 KD
h
Optimal order quantity when shortages are allowed: Q¿ =
√ 2 KD ( h+ s )
sh
Lagrange approach when multiple products have to fit in one warehouse: Q i =
¿
√ 2 K i Di
hi +2 θ c i
with θ (>0) such that the total capacity fits exactly: ∑ ci Qi=C
i
n
If the constraint is active: Q =m EOQ i where m=C / ∑ ( c i EOQi )
¿
i=1
Optimal annual costs: G ( Q )= √ 2 hKD +cD
¿
Production with finite production rate P:
D 1Q Q
Annual costs: G ( Q )= ( K + cQ+h ( P−D ) ), where D/Q is # cycles, cQ is production
Q 2P D
costs, h*1/2 is holding costs, Q/P(P-D) is maximum inventory and Q/D is cycle length.
Optimal size production run: Q=
√ 2 KD
h '
' D
where h =h(1− ) and P> D
P
Annual holding and set-up costs: √ 2 KDh '
Ordering multiple products: same cycle
2
T T
Costs per cycle:C ( T )= A+ ∑ (¿ a i+ hi Qi )=A + ∑ ( ai +hi D i )¿
i 2 i 2
A+ ∑ ai
Costs per time unit: C ( T ) = i
+ ∑ hi D i
T
T T i 2
Minimum costs at: T =√ 2 ¿¿ ¿
, Ordering multiple products: different cycles
Suppose product i is ordered every mi cycles:
Minimum costs are achieved at: T =√ 2 ¿¿ ¿
Week 2:
Lot sizing
In periodic lot sizing we consider the problem that a supplier meets in situations where
demand for products is not simply delivered from stock, but where some processing steps
have to be done before the shipment. Demand is fully known for a number of periods, the
so-called horizon, and no information is available for periods after the horizon. Two types of
costs are balanced: production set-up costs and the inventory holding costs.
Definitions and standard assumptions:
Y(t) = inventory position at the end of period t
D(t) = total demand in period t
Q(t) = production order quantity in period t
H = the number of known demand periods (horizon)
A = the fixed setup or replenishment costs
h = the carrying costs per unit of inventory per period
Rules based upon average demand
If the average demand level is D per period, the quantity is given by: EOQ = √ (¿ 2 AD /h) ¿
Rule 1: fixed quantity EOQ rule
We first determine the EOQ quantity, usually with the D-level based upon the average
demand during H periods of known demand. This quantity is rounded to the nearest integer
Qf.
Rule 2: EOQ rule
We first determine the EOQ quantity, usually with the D-level based upon the average
demand during H periods of known demand. Now, every time we produce, we will try to get
as close as possible to this quantity.
Rule 3: TEOQ fixed cycle rule (POQ)
We first determine the EOQ quantity, usually with the D-level based upon the average
demand during H periods of known demand. When we divide the EOQ quantity by the
average demand, we obtain the average time between two replenishments TEOQ. This is
rounded to the nearest integer. Every time we produce, we produce the demand for this
number of periods.