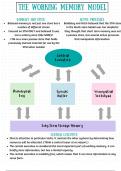
Multiple comparisons testing:
Once a one-way ANOVA rejects H0 (finds that not all group means are
equal), the next question is: which groups differ?
• Multiple comparisons testing finds the specific groups that differ from
the rest in terms of their population means.
Problem: If you run many independent hypothesis tests, the chance of
getting a Type I error (rejecting a true H0) increases.
Normally, we use a t-test to check if the means of 2 populations are
equal. But when we run an ANOVA and find that at least 1 group’s mean is
different, we naturally want to know which specific groups differ.
The obvious idea is to run t-tests for every possible pair of groups. The
problem is that running many tests increases the chance of making a
Type I error.
• This is called alpha spending or error rate inflation: the more tests you
do, the greater the overall probability of incorrectly rejecting a true null
hypothesis.
To keep the overall error rate fixed, at the desired level ( α ), we must adjust
the significance level we use for each pairwise comparison test.
Consider the following hypothesis:
If there are k groups, there are m I tests.
• Suppose each of these tests is performed at a level of significance α .
• Suppose we denote the null hypothesis of each test by
• Furthermore, assume that none of the groups differ.
6i 2 m
We expect that there is α probability to (incorrectly) conclude that at least
one group differs from the rest.
When is true:
• The chance of a false rejection is α .
• the chance of not rejecting it is 1 a .
, However:
intersection
Overall chance of rejection at 5
multiply
together
least 1 true H0 grows with m.
Thus, testing m independent hypothesis tests leads to an overall level of
significance of a
The figure below shows this function for varying number of tests, M
Once a one-way ANOVA rejects H0 (finds that not all group means are
equal), the next question is: which groups differ?
• Multiple comparisons testing finds the specific groups that differ from
the rest in terms of their population means.
Problem: If you run many independent hypothesis tests, the chance of
getting a Type I error (rejecting a true H0) increases.
Normally, we use a t-test to check if the means of 2 populations are
equal. But when we run an ANOVA and find that at least 1 group’s mean is
different, we naturally want to know which specific groups differ.
The obvious idea is to run t-tests for every possible pair of groups. The
problem is that running many tests increases the chance of making a
Type I error.
• This is called alpha spending or error rate inflation: the more tests you
do, the greater the overall probability of incorrectly rejecting a true null
hypothesis.
To keep the overall error rate fixed, at the desired level ( α ), we must adjust
the significance level we use for each pairwise comparison test.
Consider the following hypothesis:
If there are k groups, there are m I tests.
• Suppose each of these tests is performed at a level of significance α .
• Suppose we denote the null hypothesis of each test by
• Furthermore, assume that none of the groups differ.
6i 2 m
We expect that there is α probability to (incorrectly) conclude that at least
one group differs from the rest.
When is true:
• The chance of a false rejection is α .
• the chance of not rejecting it is 1 a .
, However:
intersection
Overall chance of rejection at 5
multiply
together
least 1 true H0 grows with m.
Thus, testing m independent hypothesis tests leads to an overall level of
significance of a
The figure below shows this function for varying number of tests, M