3.6.1 Periodic Motion
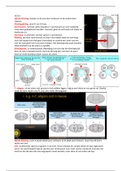
Circular Motion:
An object in uniform circular motion has a constant linear speed. However, as it is constantly
changing direction, it has a constantly changing velocity and therefore must be accelerating.
This acceleration is called the centripetal
acceleration and is perpendicular to the direction
of the linear speed/motion.
‘Centripetal’ means it acts towards the centre of
the circular path.
This acceleration is caused by a centripetal force
that also acts perpendicular to the direction of
motion (towards the centre of motion) due to
Newton’s second law.
The velocity is tangential to the circle.
Angular displacement, θ = The change in angle of a body as
it rotates around a circle.
Using arc length = rθ (in data sheet), angular displacement is given by: θ throughout this topic is in
radians.
θ = L/r, Angular displacement (rad) = Arc length (m)/ radius of orbit/ motion (m)
Angular
ω = θ/t, Angular speed (rad s-1) = Angular displacement (rad) / time (s)--> Not given speed, ω =
(Scalar)
The angle an object rotates through per unit time.
(If a complete cycle is θ=2π, then ω= 2π/T = 2πf. Also, as v = distance/time -> v = arc length/time
-> v = θr/t --> v = ωr).
ω = v/r, Angular speed = Linear speed (ms-1) /radius of orbit
ω = 2πf, frequency = number of complete revolutions per second, T = time taken for a complete revolution
1
, Centripetal acceleration, a = The acceleration of an object towards the center of a circle when an
object is in motion around a circle at constant speed.
Centripetal force, F= The resultant force towards the center of the
circle required to keep a body in uniform circular motion. It is always
directed towards the center of the body’s rotation.
a = v2/r = ω2r , Acceleration is always directed toward the center of
the circle and is perpendicular to the object’s velocity.
F = mv2/r = mω2r. It is always perpendicular to the direction of travel.
Simple Harmonic Motion (SHM):
Simple Harmonic Motion (SHM):
An oscillation in which: The acceleration of an object is proportional to its displacement from the
midpoint and acts in the opposite direction to its displacement (towards the equilibrium
position/midpoint).
If k is a constant, the restoring force, F, is given by:
F = -kx
2