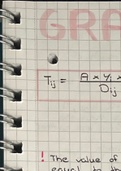Otro

Compressible Flow Lab Report

0 veces vendidas

Grado
Fluid Mechanics

Institución
Fluid Mechanics

The thermodynamic properties of the used air i.e. temperature, gas constant and pressure was used to determine the density of air as 0.95 (kg/m^3). Mas flow rate was then determined for all the cases. The mass flow rates were then used to determine the corresponding Flinger numbers for each case. T...

[Mostrar más]

Vista previa 3 fuera de 20 páginas

Ver ejemplo

Subido en 11 de septiembre de 2024
Número de páginas 20
Escrito en 2024/2025
Tipo Otro
Personaje Desconocido

fluid mechanics
mechanical engineering
electrical engineering
civil engineering
plumbing
compressible flow lab report
compressible flow fluid mechanics lab report

Institución Fluid Mechanics
Grado Fluid Mechanics

$5.49

Añadir al carrito

Guardar

100% de satisfacción garantizada
Inmediatamente disponible después del pago
Tanto en línea como en PDF
No estas atado a nada

1

COMPRESSIBLE FLOW LAB REPORT

INSTITUTION:

COURSE:

by

AUTHOR:

DATE:

, 2

INTRODUCTION

A compressible fluid is fluid whose Mach number i.e. the ratio of local velocity of fluid to the
velocity of sound at that point is greater than 0.3. A compressible fluid may be in sub-sonic,
sonic, trans-sonic, supersonic or hyper-sonic region depending on its Mach number. In a typical
analysis of a compressible fluid the fluid is assumed to be an ideal gas, one dimensional, fully
developed with negligible body forces. A compressible has both thermodynamic and dynamic
properties. The thermodynamic properties include density, temperature, enthalpy, entropy while
dynamic properties include velocity and acceleration. The thermodynamic and dynamic
properties of a compressible fluid are dependent variables which are a function of either change
in area, heat transfer to the fluid, effects of friction or effects of normal shock. Other properties
like total pressure, total temperature, mass flow per unit area and Mach number are obtained by
combining both the thermodynamic and dynamic properties of the fluid.

To easily analyze and solve compressible flow problems it’s prudent to use dimensionless
numbers like Mach number and Flinger number. The non-dimensionless numbers simplifies
physical explanations, theoretical analysis and experimental calculations. This experiment shows
how the effect of changing the duct aresa and shock waves affects the compressible flow of
fluids.

, 3

THEORETICAL ANALYSIS

One-Dimensional Flow

Steady one-dimensional flow at constant specific heats may involve area variation, wall friction,
heating, cooling, mass injection, mass removal, etc. The thermodynamic and the dynamic fluid
properties for this general type of flow vary from plane to plane normal to the flow. However, by
definition, one-dimensional flow has constant fluid properties at any chosen plane, Considering
T, P, t, p, p,V, etc. as fluid properties at any plane, we have the following equations:

Equation of state:

p=pRT....................................................................................(1)

Equation of continuity:

p AV =-- constant……………………………………. (2)

The total energy per unit mass at any plane is the sum of internal energy, flow work and kinetic
energy.
2
I.e. C T+ P + =𝑣 + C
p 2 pt = constant

By definition, the sound velocity and Mach number respectively are c=√𝛾𝑅𝑇.............(.3)

𝛾−1 2
Equation (3) by eliminating V becomes: T = t (1 + M )....................................(4)
𝛾

The isentropic law when applied to the fluid properties at the plane, gives: to, po

Equations (1), (2), (6) and (7) can be combined to give the fliegner relation.

Equations (8), (9) and (10) show that the Fliegner numbers are functions of Mach number and
ratio of specific heats only. In the case of adiabatic irreversible flow process, the Mach number
variation and total pressure distribution can be obtained from the wall static pressure

Los beneficios de comprar resúmenes en Stuvia estan en línea:

Garantiza la calidad de los comentarios

Compradores de Stuvia evaluaron más de 700.000 resúmenes. Así estas seguro que compras los mejores documentos!

Compra fácil y rápido

Puedes pagar rápidamente y en una vez con iDeal, tarjeta de crédito o con tu crédito de Stuvia. Sin tener que hacerte miembro.

Enfócate en lo más importante

Tus compañeros escriben los resúmenes. Por eso tienes la seguridad que tienes un resumen actual y confiable. Así llegas a la conclusión rapidamente!

Preguntas frecuentes

What do I get when I buy this document?

You get a PDF, available immediately after your purchase. The purchased document is accessible anytime, anywhere and indefinitely through your profile.

100% de satisfacción garantizada: ¿Cómo funciona?

Nuestra garantía de satisfacción le asegura que siempre encontrará un documento de estudio a tu medida. Tu rellenas un formulario y nuestro equipo de atención al cliente se encarga del resto.