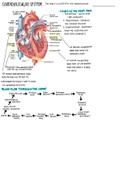
Chapter 1 Motion in a Straight Line
1.1 Distance, Position and Displacement
Describing the Motion of Objects
• Kinematics: the study of motion
• Motion: a change in an object’s location as measured by a particular observer
• Distance (d): the total length of the path travelled by an object in motion
• Direction: the line an object moves along from a particular starting point
Scalar and Vectors Quantities
• Scalar: a quantity that has only magnitude (size)
• Vector: a quantity that has magnitude (size) and direction
Position and Displacement
• Position (d): the distance and direction of an object from a reference point.
It is a vector quantity represented by the symbol ⃗⃗⃗
𝑑.
The arrow indicates the position is a vector: it has a direction as well as a magnitude.
For example:
Home is your reference point, the position of the school in Figure 2 is 500m [𝐸].
Note that the magnitude of the position is the same as the straight-line distance (500m) from home to
school, but the position also includes the direction (due to east [𝐸]).
The position of the school from point 0m can be described by the equation
𝑑𝑠𝑐ℎ𝑜𝑜𝑙 = 500𝑚 [𝐸]
Now assume that the library is your reference point, or the point 0m.
The position of the school forms the reference point (library) can be described by the equation.
𝑑𝑠𝑐ℎ𝑜𝑜𝑙 = 700𝑚 [𝑊]
1|Page
, • Displacement (∆𝑑): the change in position of an object
It is represented by the symbol 𝑑
Notice the vector arrow indicating that displacement is a vector quantity.
The triangle symbol ∆ is the Greek letter delta, always read as “change in”.
⃗⃗ = ⃗⃗𝒅𝒇𝒊𝒏𝒂𝒍 – ⃗⃗𝒅𝒊𝒏𝒊𝒕𝒊𝒂𝒍
∆𝒅
When an object changes its position more than once (experiences 2 / more displacements),
the total displacement 𝑑𝑇 of the object can be calculated by adding the displacement using the following
equation:
⃗⃗ 𝑻 = 𝒅
𝒅 ⃗⃗ 𝟏 + 𝒅
⃗⃗ 𝟐
• Vector Scale Diagrams
Vector Scale Diagram: a vector diagram drawn using a specific scale.
Directed Line Segment: a straight line between two points with a specific direction.
Summary
❖ Motion involves a change in the position of an object.
Motion can be described using mathematical relationships.
❖ A scalar is a quantity that has magnitude (size) only.
A vector is a quantity that has magnitude (size) and direction.
❖ The displacement of an object can be determined by subtracting the start position from the end
position.
❖ Total displacement can be determined by adding two / more displacements together
algebraically or by using a vector scale diagram.
❖ Vector can be added by joining them tip to tail.
2|Page
1.1 Distance, Position and Displacement
Describing the Motion of Objects
• Kinematics: the study of motion
• Motion: a change in an object’s location as measured by a particular observer
• Distance (d): the total length of the path travelled by an object in motion
• Direction: the line an object moves along from a particular starting point
Scalar and Vectors Quantities
• Scalar: a quantity that has only magnitude (size)
• Vector: a quantity that has magnitude (size) and direction
Position and Displacement
• Position (d): the distance and direction of an object from a reference point.
It is a vector quantity represented by the symbol ⃗⃗⃗
𝑑.
The arrow indicates the position is a vector: it has a direction as well as a magnitude.
For example:
Home is your reference point, the position of the school in Figure 2 is 500m [𝐸].
Note that the magnitude of the position is the same as the straight-line distance (500m) from home to
school, but the position also includes the direction (due to east [𝐸]).
The position of the school from point 0m can be described by the equation
𝑑𝑠𝑐ℎ𝑜𝑜𝑙 = 500𝑚 [𝐸]
Now assume that the library is your reference point, or the point 0m.
The position of the school forms the reference point (library) can be described by the equation.
𝑑𝑠𝑐ℎ𝑜𝑜𝑙 = 700𝑚 [𝑊]
1|Page
, • Displacement (∆𝑑): the change in position of an object
It is represented by the symbol 𝑑
Notice the vector arrow indicating that displacement is a vector quantity.
The triangle symbol ∆ is the Greek letter delta, always read as “change in”.
⃗⃗ = ⃗⃗𝒅𝒇𝒊𝒏𝒂𝒍 – ⃗⃗𝒅𝒊𝒏𝒊𝒕𝒊𝒂𝒍
∆𝒅
When an object changes its position more than once (experiences 2 / more displacements),
the total displacement 𝑑𝑇 of the object can be calculated by adding the displacement using the following
equation:
⃗⃗ 𝑻 = 𝒅
𝒅 ⃗⃗ 𝟏 + 𝒅
⃗⃗ 𝟐
• Vector Scale Diagrams
Vector Scale Diagram: a vector diagram drawn using a specific scale.
Directed Line Segment: a straight line between two points with a specific direction.
Summary
❖ Motion involves a change in the position of an object.
Motion can be described using mathematical relationships.
❖ A scalar is a quantity that has magnitude (size) only.
A vector is a quantity that has magnitude (size) and direction.
❖ The displacement of an object can be determined by subtracting the start position from the end
position.
❖ Total displacement can be determined by adding two / more displacements together
algebraically or by using a vector scale diagram.
❖ Vector can be added by joining them tip to tail.
2|Page