Summary
Samenvatting Kennisbasistoets Rekenen compleet
- Course
- Institution
- Book
Samenvatting voor de Kennisbasistoets Rekenen
[Show more]
Connected book
Book Title:
Author(s):
- Edition:
- ISBN:
- Edition:
Seller
Follow
Doortje19s
Reviews received
Content preview
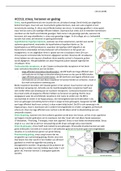
GETALLENContextualiseren Positioneren Structureren
Aantal/eenheid Meer/minder
Splitsen Ontbinden Kenschetsen
42 → 40 + 2 Keer relatie Eigenschap
groepjes
Natuurlijke getallen Reëel getallen
Hele getallen Rationele getallen
5 8 9 Kommagetallen die
-9 -100 0,5 1/3
niet repeteren
GETALLEN
- Cijfers = 0-9
- Getal = combinatie van cijfers.
- Positioneel getallenstelsel = de waarde hangt af van de positie van het getal
- Plaatswaarde/ positiewaarde = elke plaats in het getal heeft een eigen waarde
o eenheden, tientallen, honderdtallen enz. (in het getal 345 heeft 4 positiewaarde 40)
- Additief talstelsel:
o Decimaal (positioneel) getallensysteem = gebaseerd op machten van 10
o Binair getallensysteem = opgebouwd uit 0 en 1.
Hoeveelheidsgetal = geeft de hoeveelheid aan – 20 appels
Telgetal = hoeveel je er hebt geteld – 30e appel in de rij
Ordinaal getal =
Kardinaal getal =
Meetgetal = wat je gemeten hebt – 2 kg / 2 cm
Naamgetal = A20, A4-papier
Rekengetal = waarmee je rekent – 20 appels in 4 schalen = 20:4
Radix = wortel uit een getal
,DIDACTIEK - BEGRIPPEN
- Informeel = Kinderen verwerven kennis ook buiten het klaslokaal – eigen aanpak
- Formeel =op drie niveaus: concreet, schematisch en formeel.
o Getallen gebruiken zonder daarbij een model of context te hanteren - abstract: door
redenering afgeleid in plaats van door te handelen.
- Inverse relatie = bewerkingen die in bepaalde zin het omgekeerde bereikt
o Aftrekken is inverse relatie van optellen
- Automatiseren: rekenhandelingen vrijwel routinematig uitvoeren
- Memoriseren: uit het hoofd kennen van de antwoorden van sommen
STRATEGIEEN
- Rijgen = bij een optelling of aftrekking wordt het eerste getal intact gelaten en wordt het
tweede getal gesplitst.
- Splitsen = bij een optelling of aftrekking worden beide getallen gesplist in tientallen en
eenheden.
- Varia = handig oplossen met behulp van kennis, relatie tussen getallen en eigenschappen:
o Compenseren = 253 + 198 = 253 + 200 - 2
o Transformeren = 124 – 78 = 126 – 80
o Verwisselen = 125 x 7 = 7 x 125
o Aanvullen / overbruggen = 301 – 298 = uitrekenen via 298 + 3 = 301
o Verdubbelen / halveren = 16 x 25 = 8 x 50
o Gebruikmaken van de inverse relatie = 75 : 5 = uitrekenen via … x 5 = 75
Cijferend rekenen = rekenen met cijfers volgens een oplossingsmethode die opgebouwd is uit
een vaste rij elementaire handelingen, die zeker tot het ene goede antwoord voert
- Tegenovergestelde van hoofdrekenen
Algoritmisch rekenen = vast stappenplan uitvoeren (voorbeeld van cijferend rekenen)
Kolomsgewijs rekenen = fase tussen hoofdrekenen en cijferend rekenen
Handig rekenen = hoofdrekenen, eigenschappen van getallen gebruiken
Flexibel rekenen = parate kennis gebruiken, relaties tussen getallen en bewerkingen
Tellend rekenen = 18 + 7 – 19,20,21,22,23,24,25
Structurerend rekenen = grote stappen maken mbv structuur (dobbelsteen, turftabel)
MODELLEN
- Lijnmodel
- Dubbele getallenlijn
- Strook = breuken/procenten
- Rechthoekmodel = tafels, vermenigvuldigen, oppervlakte, breuken
- Pijlentaal
, EIGENSCHAPPEN
- Communicatieve eigenschap = getallen in een bewerking mag je omwisselen
- Distributieve eigenschap = getallen in een bewerking verdelen (12 x 8 → 10 x 8 + 2 x 8)
- Associatieve eigenschap = getallen in een bewerking van volgorde veranderen
- Compenseren
- Groter of kleiner = bij optellen en aftrekken
- Groter en kleiner = bij delen en vermenigvuldigen
VOORVOEGSELS METRIEKSTELSEL
10x Getal Groot 10x Getal Klein
1 Tien Deca -1 Een tiende Deci
2 Honderd Hecto -2 Een honderdste Centi
3 Duizend Kilo -3 Een duizendste Mili
6 Miljoen Mega -6 Een miljoenste Micro
9 Miljard Giga -9 Een miljardste Nano
12 Biljoen Tera -12 Een biljoenste Pico
15 Biljard Peta -15 Een biljardste Femto
18 Triljoen Exa -18 Een triljoenste Atto
21 Triljard Zetta -21 Een triljardste Zepto
24 Quadriljoen Yotta -24 Een quadriljoenste Yocto
Radixnotatie van een talstelsel = de wetenschappelijke notatie van een getal is een andere benaming voor
zwevendekommanotatie met als radix (grondtal) 10
The benefits of buying summaries with Stuvia:
Guaranteed quality through customer reviews
Stuvia customers have reviewed more than 700,000 summaries. This how you know that you are buying the best documents.
Quick and easy check-out
You can quickly pay through credit card or Stuvia-credit for the summaries. There is no membership needed.
Focus on what matters
Your fellow students write the study notes themselves, which is why the documents are always reliable and up-to-date. This ensures you quickly get to the core!
Frequently asked questions
What do I get when I buy this document?
You get a PDF, available immediately after your purchase. The purchased document is accessible anytime, anywhere and indefinitely through your profile.
Satisfaction guarantee: how does it work?
Our satisfaction guarantee ensures that you always find a study document that suits you well. You fill out a form, and our customer service team takes care of the rest.
Who am I buying these notes from?
Stuvia is a marketplace, so you are not buying this document from us, but from seller Doortje19s. Stuvia facilitates payment to the seller.
Will I be stuck with a subscription?
No, you only buy these notes for $8.02. You're not tied to anything after your purchase.
Can Stuvia be trusted?
4.6 stars on Google & Trustpilot (+1000 reviews)
73243 documents were sold in the last 30 days
Founded in 2010, the go-to place to buy study notes for 14 years now