Class notes
Sucesiones y series
- Course
- Institution
Apuntes de clase acerca de las series y sucesiones, con los tipos conocidos y métodos para resolverlas
[Show more]
Seller
Follow
anadueas
Content preview
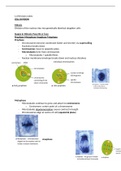
, ={ 4K # 3Pa.
.
.
SERIES Y SUCESIONES
SUCESIONES
Definición : una sucesión de números reales es una aplicación f://V-IR.si para cada n EIN ,
es flnt = an ,
derrotaremos a dicha sucesión de números reales
por { an } NEN ,
donde an lo
denominaremos término general
Podemos expresar una sucesión :
2N
De explícita
-
manera : an =
( 1 + n )
-
Mediante sus primeros términos :
1 ,
4/3 ,
° /
y ,
8/5 . . .
-
De forma recurrente : a ,
= 1 , Ann = 1 + an
Monotonía : sea la sucesión { an } nen .
Diremos que :
•
Es creciente si an E Anu ,
ltne IN .
-
Es estrictamente creciente si an
<
Ann ,
ltne IN .
•
Es decreciente si an ? anti ,
ltn EN
•
Es estrictamente decreciente si an > an + , ,
U-ne.IN .
Acotación : sea la sucesión { an } nene . Diremos que :
•
Está acotada superiormente si JM c- IR tal que an EM One IN
-
Está acotada inferiormente si 3m E IR tai que an In One IN
•
Está acatada si está acotada superiormente e inferiormente .
LIMITE DE UNA SUCESIÓN
Convergencia : diremos que una sucesión { anlnen converge a l E IR ( o su límite es l cuando
n tiende a más infinito ) lo derrotaremos por :
,
y
him an = l o { an } →
l
n → o
si te > 0 ,
existe no tal que Un >
no ,
se verifica tan -
el < E
Divergencia :
Definición : diremos que una sucesión tan } diverge a más infinito ( o su límite es + ao
cuando n tiende a más infinitos ,
y lo derrotaremos por :
him an = + a ó { an } → + o
n → o
Si UM > 0 ,
existe no C- IN , tal que Un Z no , an > M .
Definición : diremos que una sucesión tan } diverge a menos infinito ( o su límite es -
ao
cuando n tiende a más infinitos ,
y lo derrotaremos por :
him an = -
ao ó { an } → -
ao
n → ao
Si UM > 0 ,
existe no C- IN , tal que Un Z no , ane -
M .
Oscilante : diremos que una sucesión es oscilante si no converge ni
diverge .
The benefits of buying summaries with Stuvia:
Guaranteed quality through customer reviews
Stuvia customers have reviewed more than 700,000 summaries. This how you know that you are buying the best documents.
Quick and easy check-out
You can quickly pay through credit card or Stuvia-credit for the summaries. There is no membership needed.
Focus on what matters
Your fellow students write the study notes themselves, which is why the documents are always reliable and up-to-date. This ensures you quickly get to the core!
Frequently asked questions
What do I get when I buy this document?
You get a PDF, available immediately after your purchase. The purchased document is accessible anytime, anywhere and indefinitely through your profile.
Satisfaction guarantee: how does it work?
Our satisfaction guarantee ensures that you always find a study document that suits you well. You fill out a form, and our customer service team takes care of the rest.
Who am I buying these notes from?
Stuvia is a marketplace, so you are not buying this document from us, but from seller anadueas. Stuvia facilitates payment to the seller.
Will I be stuck with a subscription?
No, you only buy these notes for $7.49. You're not tied to anything after your purchase.
Can Stuvia be trusted?
4.6 stars on Google & Trustpilot (+1000 reviews)
64438 documents were sold in the last 30 days
Founded in 2010, the go-to place to buy study notes for 14 years now