Notizen

empirische Verteilungsfunktion

0 mal verkauft

Kurs
Statistik

Hochschule
Hochschule Darmstadt

Die empirische Verteilungsfunktion wird durch das Aufsummieren der relativen Häufigkeiten der Beobachtungen in der Stichprobe gebildet. Dabei wird jedem Wert der Stichprobe eine relative Häufigkeit zugewiesen, die angibt, wie oft dieser Wert in der Stichprobe auftritt. Diese Häufigkeiten werden ...

[ Mehr anzeigen ]

vorschau 1 aus 3 Seiten

Zum Beispiel

Hochgeladen auf 11. mai 2023
Anzahl der Seiten 3
geschrieben in 2022/2023
Typ Notizen
Professor(en) Christoph becker und florence micol
Enthält Alle klassen

statistik
wing
hda
empirische verteilungsfunktion

30,49 €

In den Einkaufswagen

Zur Wunschliste hinzufügen

100% Zufriedenheitsgarantie
Sofort verfügbar nach Zahlung
Sowohl online als auch als PDF
Du bist an nichts gebunden

Die empirische Verteilungsfunktion (auch empirische Verteilungsfunktion oder ECDF)
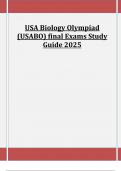
ist eine Funktion, die die kumulative Verteilungsfunktion (CDF) einer Stichprobe
approximiert. Sie ist eine Schätzung der wahren CDF einer Zufallsvariablen, die
aufgrund der begrenzten Anzahl von Beobachtungen nicht direkt bestimmt werden
kann.
Die empirische Verteilungsfunktion wird durch das Aufsummieren der relativen
Häufigkeiten der Beobachtungen in der Stichprobe gebildet. Dabei wird jedem Wert
der Stichprobe eine relative Häufigkeit zugewiesen, die angibt, wie oft dieser Wert in
der Stichprobe auftritt. Diese Häufigkeiten werden dann aufsummiert, um die
empirische Verteilungsfunktion zu erhalten.
Die empirische Verteilungsfunktion ist eine Schritt-förmige Funktion, bei der jeder
Sprungpunkt einem beobachteten Wert der Zufallsvariablen entspricht. Sie hat den
Wert 0 am kleinsten beobachteten Wert und den Wert 1 am größten beobachteten
Wert.
Die empirische Verteilungsfunktion hat viele Anwendungen in der Statistik und
Datenanalyse. Sie wird oft verwendet, um die Verteilung von Daten zu untersuchen,
um statistische Tests durchzuführen oder um Schätzungen von Parametern der
zugrunde liegenden Verteilung durchzuführen. Sie kann auch verwendet werden, um
die Wahrscheinlichkeit eines bestimmten Wertes oder Intervalls zu berechnen oder
um die Abweichung der empirischen Verteilung von der theoretischen Verteilung zu
messen.
Die empirische Verteilungsfunktion kann einfach graphisch dargestellt werden, indem
man die beobachteten Werte auf der horizontalen Achse und die kumulativen
relativen Häufigkeiten auf der vertikalen Achse aufträgt. Diese Darstellung wird als
empirische Verteilungsfunktion oder Ogive bezeichnet.
Insgesamt ist die empirische Verteilungsfunktion eine wichtige Methode in der
Statistik und Datenanalyse, die es ermöglicht, Aussagen über die Verteilung von Daten
zu treffen, auch wenn die zugrunde liegende Verteilung unbekannt oder komplex ist.
Eine wichtige Eigenschaft der empirischen Verteilungsfunktion ist, dass sie eine
konsistente Schätzung der wahren Verteilungsfunktion darstellt, d.h. sie konvergiert in
der Wahrscheinlichkeit gegen die tatsächliche Verteilungsfunktion, wenn die
Stichprobengröße gegen unendlich geht. Diese Eigenschaft ist besonders nützlich, da
sie es ermöglicht, statistische Tests durchzuführen und Schätzungen von Parametern
der wahren Verteilung zu machen, ohne die genaue Form der Verteilung zu kennen.
Eine weitere wichtige Anwendung der empirischen Verteilungsfunktion ist die
Berechnung von Quantilen. Ein Quantil ist ein Wert, bei dem eine bestimmte
proportionale Aufteilung der Daten erfolgt, z.B. das 25. oder das 75. Perzentil. Das k-
te empirische Quantil wird durch die Bestimmung des Werts x_k berechnet, bei dem

Alle Vorteile der Zusammenfassungen von Stuvia auf einen Blick:

Garantiert gute Qualität durch Reviews

Stuvia Verkäufer haben mehr als 700.000 Zusammenfassungen beurteilt. Deshalb weißt du dass du das beste Dokument kaufst.

Schnell und einfach kaufen

Man bezahlt schnell und einfach mit iDeal, Kreditkarte oder Stuvia-Kredit für die Zusammenfassungen. Man braucht keine Mitgliedschaft.

Konzentration auf den Kern der Sache

Deine Mitstudenten schreiben die Zusammenfassungen. Deshalb enthalten die Zusammenfassungen immer aktuelle, zuverlässige und up-to-date Informationen. Damit kommst du schnell zum Kern der Sache.

Häufig gestellte Fragen

Was bekomme ich, wenn ich dieses Dokument kaufe?

Du erhältst eine PDF-Datei, die sofort nach dem Kauf verfügbar ist. Das gekaufte Dokument ist jederzeit, überall und unbegrenzt über dein Profil zugänglich.

Zufriedenheitsgarantie: Wie funktioniert das?

Unsere Zufriedenheitsgarantie sorgt dafür, dass du immer eine Lernunterlage findest, die zu dir passt. Du füllst ein Formular aus und unser Kundendienstteam kümmert sich um den Rest.

Wem kaufe ich diese Zusammenfassung ab?

Stuvia ist ein Marktplatz, du kaufst dieses Dokument also nicht von uns, sondern vom Verkäufer fanatesfamariam. Stuvia erleichtert die Zahlung an den Verkäufer.

Werde ich an ein Abonnement gebunden sein?

Nein, du kaufst diese Zusammenfassung nur für 30,49 €. Du bist nach deinem Kauf an nichts gebunden.

Kann man Stuvia trauen?

4.6 Sterne auf Google & Trustpilot (+1000 reviews)

45.681 Zusammenfassungen wurden in den letzten 30 Tagen verkauft

Gegründet 2010, seit 15 Jahren die erste Adresse für Zusammenfassungen

Starte mit dem Verkauf