Fundamentals of computational
thinking
Last edited time @November 13, 2023 9:43 PM
Status Done
Problem solving and abstraction
Logical reasoning → The process of using a given set of facts to determine whether
new facts are true or false.
algorithm → a sequence of instructions.
representational abstraction → The process of removing unnecessary details so that
only information that is required to solve the problem remains.
Abstraction by generalisation → the concept of reducing problems by putting similar
aspects of a problem into hierarchical categories. This is called top-down design.
functional abstraction → breaking down a complex problem into a series of reusable
functions.
data abstraction → hiding how data is represented so that it is easier to build a new
kind of data object. This is done easily within OOP using getters, setters and private
members.
information hiding → the process of hiding all details of an object that do not
contribute to its essential characteristics. An example of this is using a GUI, where it
hides how the objects/classes are actually behaving.
decomposition → breaking down a large task into a series of smaller tasks.
Composition → building up a whole system from smaller parts. The opposite of
decomposition.
Finite state machines
Finite state machine → Any device that stores its current state and whose state can
change as the result of an input. They are commonly used as a conceptual model for
describing systems.
State transition diagrams
Fundamentals of computational thinking 1
, State transition diagram → A visual representation of a finite state machine. One can
be seen below:
In the diagram above:
S0 → The idle state. This is the state before an input has been entered into the
finite state machine. It is also the start point of the machine
S1 and S3 → States 1 and 3.
S2 → The accepting state. This identifies whether or not an input has been
accepted within the finite state machine. A valid finite state machine does not
require an accepting state.
In a finite state machine, the labels on the arrows indicate the state to go to based off
of the input at that state. For example, if on S1, got to S3 if a 0 is inputted.
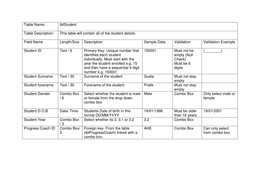
This data can also be represented in a tabular form.
State transition table → A tabular representation of a finite state machine, show
inputs current state and next state.
The outline of a table is below:
State Input Next State
Finite state machine with outputs
Mealy machine → A finite state machine with outputs. An example is shown below:
Fundamentals of computational thinking 2