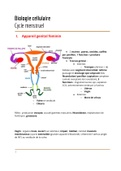
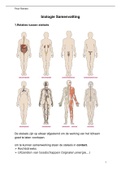
pedagogen: HC
Hoofdstuk 1: verdeling van gegevens (1 variabele)
1. Het gegevensrooster
2. 2 types van variabelen
A. Onafhankelijke & afhankelijke variabelen
B. Discrete & continue variabelen
C. Kwalitatieve & kwantitatieve variabelen
hiërarchie: kwalordinaalkwant
3. Het beschrijven van 1 variabele
A. Via tabellen
Frequentietabellen:
f(X) = frequentie, hoe vaak komt score voor
p(X)= relatieve frequentie/proportie v score op X (f(X)/n)
F(X)= cumulatieve frequentie, totaal aantal scores ≤ die bep score
Altijd eerst frequentie nodig!
Bovenste getal in tabel = n
P(X)= relatieve cumulatieve frequentie (F(X)/n
Kwalitatieve gegevens:
Stamdiagrammen: goede manier om individuele scores te laten zien
B. Weergeven in figuren
Zie ook BOXPLOT
Histogrammen (gegroepeerd of niet)
Staafdiagrammen
Taartdiagrammen
! let op eerlijke figuren: tips
C. Beschrijven ahv kengetallen= in 1 getal een samenvatting over data, kengetal kan betrekking hebben op 1
variabele
Percentielen: score op X waaronder TEN MINSTE een specifiek % v scores gesitueerd is (≤ ≈ F(X))
% komt niet voorscore erboven nemen (ditchsbijzijnde P(X)) groter dan percentiel
% komt wel voorkijk nr Xinterval […,…[ (+ 1 hoger nemen)daar gemiddelde van nemen
P100= hoogst geobserveerde score, P0= laagst geobserveerde score
Centrum:
Modus: score/categorie met hoogste frequentie—OP X-as zien, ook zien op stamloof
Mediaan Q2: middelste waarde, dus minstens helft v score s ligt erboven en minstens helft eronder (P50)
, Rekenkundig gemiddelde:
formule 1 score
formule voor alle scores frequentietabel . f(X) : n
formule voor relatieve frequenties . p(X)hier weet je n niet dus zegt niet veel over data
! gemiddelde van lineair getransformeerde scores lineaire transformatie op scores
kan je ook meteen toepassen op rekenkundig gemiddelde v ongetransformeerde scores
Spreidingbeter beeld over data (aangezien Me of gemiddelde niet altijd alles zeggen)
Bereik (nadeel: gevoelig vr uitschieters)dus interkwartielbereik (of interkwartielafstand)
Variantie (hoe verspreid scores liggen rond gemiddelde) en
standaardafwijking/standaarddeviatie ( oorspronkelijke meeteenheid)
Transformatie (+&- gn invloed), wel *& :
Vergelijken met anderenSD standardiseren (gemiddelde=0, SD=1)
= standaardscore/z-score, hvl SD je boven/onder gemiddelde scoort
Hoe verhoudt X tov Y: bv beiden scores even extreem want zelfde SD
Scheefheid: Wnnr gemiddelde en SD zelfde is kan 2 versch datasets er toch anders uitziendoor
scheefheid
A3<0 negatief scheve verdeling of links scheve verdeling
Unimodaal: gemiddeld < mediaan < modus
a3=0 symmetrische verdeling
unimodaal: gemiddeld = mediaan = modus
a3>0 positief scheve verdeling of rechts scheve verdeling
unimodaal: gemiddelde>mediaan>modus
BOXPLOT (zowel voor kengetallen als figuren)
Zegt iets over scheefheid
P25 meer linksrechts positieve verdeling OF P25 meer rechterkant links negatieve verdeling
D. Normale verdelingen
Ideale verdeling grijpenmet functie (versch modellen, meest basic= normale verdeling bepaald door
gemiddelde en SD)
Functievoorschrift
Gebruik
= tekenen v normale verdeling bovenop relatieve frequentiehistogram (= dichtheidskrommen)
Opp berekenen:
Variabele standaardnormaal verdeeldtabel A
Variabele normaal verdeeldstandardiseren (Z-score) tabel A
, Hoofdstuk 2: relaties tussen 2 variabelen
1. Het beschrijven van 2 variabelen
A. Via Tabellen (kwalitatieve/ordinale variabelen) – kruistabel: voor 2 kwal var OF 2 kwant met bep aantal waarden
Rijvariabele en kolomvariabele
Gezamenlijke, marginale en totale frequentie
Relatieve frequentie: 3 soorten
Celsgewijze p(X) – celpercentages
Rijsgewijze p(X) – rijpercentages
Kolomsgewijze p(X) - kolompercentages
Cumulatieve en relatieve cumulatieve frequentie
Aflezen v samenhang uit een kruistabel
Kan enkel via verschillende rij/kolomsgewijze condiotonele relatieve frequentieverdeling ((2) en 3))
Samenhang en voorspelbaarheid
Voorspelling enkel bij samenhang die leidt tot kleinste aantal fouten (zie C correlatie)
B. Via figuren
Voor 2 kwalitatieve variabelen:
Taartdiagrammen, gegroepeerd staafdiagram, gegevenskaarten
Voor 1 kwalitatieve en 1 kwantitatieve variabele
Histogrammen, zij-aan-zij boxplot
Voor 2 kwantitatieve variabelen
Spreidingsdiagram
C. Via kengetallen (correlatie)
Pearson product- moment correlatiecoëfficiënt= maat voor lineaire samenhang tss 2
kwantitatieve variabelen
Productensomco-variantieproduct-moment correlatiecoëfficiënt
Eigenschap: RXX= 1 ; RXY= communatief
Interpretatie pearson product moment correlatiecoefficient
Waarde zegt iets over: aard, richting, sterkte
Sterkte: 0-.20 (zwak), .20-.40 (matig), .40-1.00 (sterk)
! teken altijd grafiek want dataverdeling kan heel anders zijn bij zelfde r
Misverstanden
R is niet per definitie Transitief
R is geen maat voor niet-lineaire samenhang
R w niet beïnvloed door zuiver positief/negatief lineaire transformaties vd variabelen
R zegt niets over mechanisme achter de lineaire samenhang (ze mogen dus niet causaal geïnterpreteerd
w)Versch mechanismen:
Spurious correlation