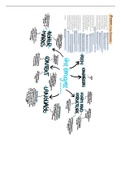
Q1 [10 points]. Consider the goal model below. Use the qualitative bottom-up label propagation technique
by Sebastiani et al. to determine the final labeling concerning evidence of satisfaction and evidence of denial
for each goal in the model. The initial assignment is listed under the figure.
Hint: use the table that was shown in class to avoid mistakes: column 1 –> goal ID, columns 2-3 --> input S
and input D, columns 4-5 --> round 1 S and D, …
Grading: 10 points = correct answer, correct method; 7 points = correct answer, unclear method; 7 points =
correct method, trivial error in the propagation; 5 points = correct method, significant error or multiple errors
in the propagation; 3 points = incorrect answer, unclear or incorrect method; 0 points otherwise.
Initial value assignment: PD(G4), FD(G5), FS(G6), PD(G6), FD(G8), FS(G9), PS(G10)
Page | 1
, Q2 [11 points]. Consider the goal-oriented version of the next release problem for software products
described in the paper “Goal-oriented release planning: A new life for goal models”. Analyze the goal model
in the figure below, and consider the following optimization scheme:
Obj1: Maximize the sum of (value-cost) for the goals in the release candidate µ:
𝑂𝑏𝑗1 = 𝑚𝑎𝑥𝑖𝑚𝑖𝑧𝑒 ∑(𝐺. 𝑣𝑎𝑙𝑢𝑒 − 𝐺. 𝑐𝑜𝑠𝑡)
𝐺∈𝜇
Obj2: If a unique optimal solution cannot be identified according to Obj1, then maximize (number of "V+" +
number of "C—") connecting goals in the solution:
𝑂𝑏𝑗2 = 𝑚𝑎𝑥𝑖𝑚𝑖𝑧𝑒 (|𝑉 + | + |𝐶 − |)
2a [8 points]. Determine the optimal release candidate µ that satisfies A and F. Show your calculations.
Possible release candidates, with H and I being always included.
J K
B y
D y y
E y
BD y
BE
DE y
BDE
H,I are mandatory, and the solutions differ for
BJ = 5+8
DJ = 4+8
DK = 4+7
EK = 6+7
BDJ = 5+4+8
DEK = 4+6+7
Page | 2
by Sebastiani et al. to determine the final labeling concerning evidence of satisfaction and evidence of denial
for each goal in the model. The initial assignment is listed under the figure.
Hint: use the table that was shown in class to avoid mistakes: column 1 –> goal ID, columns 2-3 --> input S
and input D, columns 4-5 --> round 1 S and D, …
Grading: 10 points = correct answer, correct method; 7 points = correct answer, unclear method; 7 points =
correct method, trivial error in the propagation; 5 points = correct method, significant error or multiple errors
in the propagation; 3 points = incorrect answer, unclear or incorrect method; 0 points otherwise.
Initial value assignment: PD(G4), FD(G5), FS(G6), PD(G6), FD(G8), FS(G9), PS(G10)
Page | 1
, Q2 [11 points]. Consider the goal-oriented version of the next release problem for software products
described in the paper “Goal-oriented release planning: A new life for goal models”. Analyze the goal model
in the figure below, and consider the following optimization scheme:
Obj1: Maximize the sum of (value-cost) for the goals in the release candidate µ:
𝑂𝑏𝑗1 = 𝑚𝑎𝑥𝑖𝑚𝑖𝑧𝑒 ∑(𝐺. 𝑣𝑎𝑙𝑢𝑒 − 𝐺. 𝑐𝑜𝑠𝑡)
𝐺∈𝜇
Obj2: If a unique optimal solution cannot be identified according to Obj1, then maximize (number of "V+" +
number of "C—") connecting goals in the solution:
𝑂𝑏𝑗2 = 𝑚𝑎𝑥𝑖𝑚𝑖𝑧𝑒 (|𝑉 + | + |𝐶 − |)
2a [8 points]. Determine the optimal release candidate µ that satisfies A and F. Show your calculations.
Possible release candidates, with H and I being always included.
J K
B y
D y y
E y
BD y
BE
DE y
BDE
H,I are mandatory, and the solutions differ for
BJ = 5+8
DJ = 4+8
DK = 4+7
EK = 6+7
BDJ = 5+4+8
DEK = 4+6+7
Page | 2