, Buch 5 201 Nr 1-4 .
13.06.2024
Mxy
i
2 ..
O 1 :
Y
i23 3x2
7
Z
Ch
3
+
D
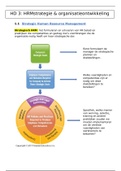
A liegt in der evs Ebene
Bliegt in der X1xz-Ebene W
Cliegt in der x1x2-Ebene
D liegt auf der 3-Achse ~
D + (12/3)
FE4/0/1)
, 13.06.2024 B . S . 201 Nr2
& PC3/1/0) Vinx1-x b) P(4/3/0) vin +1
-
x
PC3/BJV in +1-43
pC0/1/3) V in X2-13 B C4/vin
& PG2/1/0) vinx1 -x2 DPC12/4/0) Vinx1 -
x
↑ (-21017) v in ↑ (1 21010) Vin +1-43
+1-43 ,
PCOM/7)Vin x2-x3 PCO/4/8) Vin x2-x3
Nr3
D Dass es in der Xz-Xz Ebene liegt
* =0 Dass es in der xy-z Ebene liegt
↓ = 0 Dass es in der 41-x2 Ebene liegt
z
Dres liegt auf der -Achse
0=3 Nr4
xy =0
X1 Xz Ebene Ebene
-
Xz Xz
-
-
G(1/110) ~ E,Y
F(1/210) v G(010, 5 /-0 5) ~ ,
EC-41-110) V
, 13.06.2024
Kl. 11 Vektorgeometrie Datum:
Punkte im Raum Informationsblatt
Zur Angabe der Lage von Punkten im Raum kann man ein
dreidimensionales kartesisches Koordinatensystem verwenden. Es
wird durch 3 Zahlengeraden festgelegt, die paarweise aufeinander
senkrecht stehen, die Koordinatenachsen.
Ihr gemeinsamer Nullpunkt ist der Ursprung O. -
Die Koordinatenachsen werden als x1-Achse (zeigt nach vorne), &
x2-Achse (zeigt nach rechts) und x3-Achse (zeigt nach oben)
bezeichnet. Je zwei Koordinatenachsen spannen eine
Koordinatenebene (die x1x2-Ebene, x2x3-Ebene, x1x3-Ebene) auf.
Die Lage eines Punktes P gibt man mit seinen drei Koordinaten P (x1Ix2Ix3) an.
Die Punkte P (x1Ix2Ix3) liegen in der
x1x2-Ebene x3=0
x2x3-Ebene, wenn x1=0
x1x3-Ebene x2=0 .
Die Punkte P (x1Ix2Ix3) liegen auf der
x1-Achse x2=0 und x3=0
x2-Achse, wenn x1=0 und x3=0
x3-Achse x1=0 und x2=0 .
Zur Darstellung des Koordinatensystems zeichnet man die
positive x1-Achse in einem Winkel von 135° gegenüber der
x2-Achse.
Dabei wählt man für die x2-Achse und x3-Achse: 1 LE=1cm
für die x1-Achse: 1LE = 0,5√2 cm (d.h.
eine Karokästchendiagonale).
13.06.2024
Mxy
i
2 ..
O 1 :
Y
i23 3x2
7
Z
Ch
3
+
D
A liegt in der evs Ebene
Bliegt in der X1xz-Ebene W
Cliegt in der x1x2-Ebene
D liegt auf der 3-Achse ~
D + (12/3)
FE4/0/1)
, 13.06.2024 B . S . 201 Nr2
& PC3/1/0) Vinx1-x b) P(4/3/0) vin +1
-
x
PC3/BJV in +1-43
pC0/1/3) V in X2-13 B C4/vin
& PG2/1/0) vinx1 -x2 DPC12/4/0) Vinx1 -
x
↑ (-21017) v in ↑ (1 21010) Vin +1-43
+1-43 ,
PCOM/7)Vin x2-x3 PCO/4/8) Vin x2-x3
Nr3
D Dass es in der Xz-Xz Ebene liegt
* =0 Dass es in der xy-z Ebene liegt
↓ = 0 Dass es in der 41-x2 Ebene liegt
z
Dres liegt auf der -Achse
0=3 Nr4
xy =0
X1 Xz Ebene Ebene
-
Xz Xz
-
-
G(1/110) ~ E,Y
F(1/210) v G(010, 5 /-0 5) ~ ,
EC-41-110) V
, 13.06.2024
Kl. 11 Vektorgeometrie Datum:
Punkte im Raum Informationsblatt
Zur Angabe der Lage von Punkten im Raum kann man ein
dreidimensionales kartesisches Koordinatensystem verwenden. Es
wird durch 3 Zahlengeraden festgelegt, die paarweise aufeinander
senkrecht stehen, die Koordinatenachsen.
Ihr gemeinsamer Nullpunkt ist der Ursprung O. -
Die Koordinatenachsen werden als x1-Achse (zeigt nach vorne), &
x2-Achse (zeigt nach rechts) und x3-Achse (zeigt nach oben)
bezeichnet. Je zwei Koordinatenachsen spannen eine
Koordinatenebene (die x1x2-Ebene, x2x3-Ebene, x1x3-Ebene) auf.
Die Lage eines Punktes P gibt man mit seinen drei Koordinaten P (x1Ix2Ix3) an.
Die Punkte P (x1Ix2Ix3) liegen in der
x1x2-Ebene x3=0
x2x3-Ebene, wenn x1=0
x1x3-Ebene x2=0 .
Die Punkte P (x1Ix2Ix3) liegen auf der
x1-Achse x2=0 und x3=0
x2-Achse, wenn x1=0 und x3=0
x3-Achse x1=0 und x2=0 .
Zur Darstellung des Koordinatensystems zeichnet man die
positive x1-Achse in einem Winkel von 135° gegenüber der
x2-Achse.
Dabei wählt man für die x2-Achse und x3-Achse: 1 LE=1cm
für die x1-Achse: 1LE = 0,5√2 cm (d.h.
eine Karokästchendiagonale).