Videocolleges Toetsende Statistiek
Aard: beschrijven van de significante percentageverschillen (percentageverschil = d%)
Sterkte: samenhangsmaat (zie hierboven)
Significantie: verband mogen generaliseren naar de populatie toetsen
Blok 1: algemene toetsingtheorie en toetsen van 1 gemiddelde
Steekproevenverdeling
µ = populatie gemiddelde
x̄ = steekproef gemiddelde
- Meerdere steekproef gemiddelden berekenen op basis van toeval
- Deze steekproefgemiddelden weergeven in een histogram deze
frequentieverdeling = steekproevenverdeling
Sampling distributions site
- Bovenste grafiek: verdeling van populatie
- Tweede grafiek: steekproef (steekproef kan 1, 5, 10.000 en 100.000 gedaan worden)
- Derde grafiek: steekproef gemiddelde
Beschrijving van de verdeling in de populatie
Populatie Steekproevenverdeling van
het gemiddelde
Centrum Populatiegemiddelde (µ) Verwachtingswaarde E(x̄ )
E(x̄ ) = µ
Spreiding Standaardafwijking (σ) Standaardfout
Vorm Maakt niet uit Normaalverdeling mits
n > 30 Centrale
, limietstelling: Hiermee
wordt bedoeld dat de vorm
van de
steekproevenverdeling van
het gemiddelde een
normaalverdeling (Z-
verdeling) is, wanneer de
afzonderlijke steekproeven
voldoende groot zijn: n≥30.
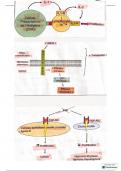
Toetsingprincipe
Hypothesen
- Onderzoekshypothese: nederlander is gemiddeld ouder dan in 1899
- Statistische hypothesen
o Alternatieve hypothese Ha : µ > 27,1
o Nulhypothese H0 : µ = 27,1
Is altijd conservatief
Falsificeren
- Altijd uitgaan van H0
- Doel onderzoek Nulhypothese verwerpen
Overschrijdingskans (p)
- Kans op gevonden steekproefresultaat (of extremer) als H0 waar is
o Grote kans H0 behouden
o Kleine kans H0 verwerpen
- Steekproevenverdeling nodig om deze kans te berekenen
Stappenplan
- Steekproevenverdeling heeft vorm Z-verdeling
- x̄ omzetten in toetsingsgrootheid Z
x̄−µ
o Z=
standaardfout
- Overschrijdingskans p bepalen
o Z-tabel
o SPSS: “Sig”
- Significantieniveau: criterium waartegen p wordt beoordeeld
o Zelf te bepalen, maar = 0,10, = 0,05 of = 0,01 gebruikelijk
- Conclusie trekken
o H0 verwerpen als:
Toetsingsresultaat in het verwerpingsgebied ligt
P<
, -
Toetsingstheorie
SPSS
- Analyze Compare Means and Proportions One Sample T-test test value: µ
invullen
o In SPSS29: kan eenzijdig en tweezijdig te zien zijn
o SPSS27: alleen tweezijdig (Sig)
Waarom doet SPSS een t-toets?
- Z-verdeling en t-verdeling vaste vormen
- T-verdeling
o Tabel A.2 Field
( x̄ −µ)
o t=
Std . Error Mean
o Vorm hangt af van vrijheidsgraden (df)
o df = n-1
o Hangt dus af van steekproefomvang
- Vorm steekproevenverdeling van het gemiddelde
o Z-verdeling als bekend is én n>30
o T-verdeling als onbekend is
Toetsing uitwerken mbv p-waarde
Steekproefresultaat (x̄ ) toetswaarde (t (en df)) p (one-sided p) p vs conclusie
Toetsing uitwerken mbv kritische toetswaarde (tabel A.2)
Steekproefresultaat toetswaarde tc.v.(aflezen bij de waarde van df) t vs tc.v.
conclusie
- t > tc.v. H0 verwerpen
Een en tweezijdig toetsen
Stappenplan hypothesetoetsing
- Formuleren H0 en Ha
- Kies significantieniveau ()
- Steekproefresultaat (x̄ ) (controleren: in lijn met de Ha?)
- Toetsingsgrootheid (t)
- Overschrijdingskans p (een- of tweezijdig)
- Vergelijken p vs
- Conclusie H0
- Inhoudelijke conclusie
Aard: beschrijven van de significante percentageverschillen (percentageverschil = d%)
Sterkte: samenhangsmaat (zie hierboven)
Significantie: verband mogen generaliseren naar de populatie toetsen
Blok 1: algemene toetsingtheorie en toetsen van 1 gemiddelde
Steekproevenverdeling
µ = populatie gemiddelde
x̄ = steekproef gemiddelde
- Meerdere steekproef gemiddelden berekenen op basis van toeval
- Deze steekproefgemiddelden weergeven in een histogram deze
frequentieverdeling = steekproevenverdeling
Sampling distributions site
- Bovenste grafiek: verdeling van populatie
- Tweede grafiek: steekproef (steekproef kan 1, 5, 10.000 en 100.000 gedaan worden)
- Derde grafiek: steekproef gemiddelde
Beschrijving van de verdeling in de populatie
Populatie Steekproevenverdeling van
het gemiddelde
Centrum Populatiegemiddelde (µ) Verwachtingswaarde E(x̄ )
E(x̄ ) = µ
Spreiding Standaardafwijking (σ) Standaardfout
Vorm Maakt niet uit Normaalverdeling mits
n > 30 Centrale
, limietstelling: Hiermee
wordt bedoeld dat de vorm
van de
steekproevenverdeling van
het gemiddelde een
normaalverdeling (Z-
verdeling) is, wanneer de
afzonderlijke steekproeven
voldoende groot zijn: n≥30.
Toetsingprincipe
Hypothesen
- Onderzoekshypothese: nederlander is gemiddeld ouder dan in 1899
- Statistische hypothesen
o Alternatieve hypothese Ha : µ > 27,1
o Nulhypothese H0 : µ = 27,1
Is altijd conservatief
Falsificeren
- Altijd uitgaan van H0
- Doel onderzoek Nulhypothese verwerpen
Overschrijdingskans (p)
- Kans op gevonden steekproefresultaat (of extremer) als H0 waar is
o Grote kans H0 behouden
o Kleine kans H0 verwerpen
- Steekproevenverdeling nodig om deze kans te berekenen
Stappenplan
- Steekproevenverdeling heeft vorm Z-verdeling
- x̄ omzetten in toetsingsgrootheid Z
x̄−µ
o Z=
standaardfout
- Overschrijdingskans p bepalen
o Z-tabel
o SPSS: “Sig”
- Significantieniveau: criterium waartegen p wordt beoordeeld
o Zelf te bepalen, maar = 0,10, = 0,05 of = 0,01 gebruikelijk
- Conclusie trekken
o H0 verwerpen als:
Toetsingsresultaat in het verwerpingsgebied ligt
P<
, -
Toetsingstheorie
SPSS
- Analyze Compare Means and Proportions One Sample T-test test value: µ
invullen
o In SPSS29: kan eenzijdig en tweezijdig te zien zijn
o SPSS27: alleen tweezijdig (Sig)
Waarom doet SPSS een t-toets?
- Z-verdeling en t-verdeling vaste vormen
- T-verdeling
o Tabel A.2 Field
( x̄ −µ)
o t=
Std . Error Mean
o Vorm hangt af van vrijheidsgraden (df)
o df = n-1
o Hangt dus af van steekproefomvang
- Vorm steekproevenverdeling van het gemiddelde
o Z-verdeling als bekend is én n>30
o T-verdeling als onbekend is
Toetsing uitwerken mbv p-waarde
Steekproefresultaat (x̄ ) toetswaarde (t (en df)) p (one-sided p) p vs conclusie
Toetsing uitwerken mbv kritische toetswaarde (tabel A.2)
Steekproefresultaat toetswaarde tc.v.(aflezen bij de waarde van df) t vs tc.v.
conclusie
- t > tc.v. H0 verwerpen
Een en tweezijdig toetsen
Stappenplan hypothesetoetsing
- Formuleren H0 en Ha
- Kies significantieniveau ()
- Steekproefresultaat (x̄ ) (controleren: in lijn met de Ha?)
- Toetsingsgrootheid (t)
- Overschrijdingskans p (een- of tweezijdig)
- Vergelijken p vs
- Conclusie H0
- Inhoudelijke conclusie