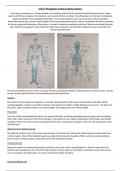
= algemene relatie tussen elektrische lading en elektrisch veld
ELEKTRISCHE FLUX
= Elektrisch veld dat door een bepaald oppervlak gaat (veldlijnen)
Flux door oppervlak is RE met aantal veldlijnen (N) dat dit oppervlak snijdt
N ∝ EA⊥ = фE
HOMOGEEN ELEKTRISCH VELD MET VLAK OPPERVLAKTE A
Oppervlak A
Elektrisch veld E
Elektrische flux фE
Hoek Ѳ tussen richting van het elektrisch veld en een lijn ⊥ op het opp
NIET HOMOGEEN ELEKTRISCH VELD ZONDER VLAK OPPERVLAK
Veld verdelen in n kleine oppervlakken integraal berekenen
Wet van Gauss: totale flux door een gesloten oppervlak (willekeurige vorm)
Oppervlak A
Elektrisch veld E
Elektrische flux фE
Integraal van een gesloten oppervlak dat een volume volledig insluit
Eigenschappen:
Richting van A (of dA) is naar buiten gericht vanuit het omsloten volume
Hoek Ѳ tussen E en A altijd kleiner dan π/2 (90°) cos Ѳ = 0
≠ 0 tenminste 1 lijn binnen het oppervlak begint/eindigt
De flux die een gesloten volume binnenkomt is negatief, de flux die het volume
verlaat is positief
1
, WET VAN GAUSS VS WET VAN COULOMB
WET VAN GAUSS
= exacte relatie tussen de elektrische flux door een gesloten oppervlak en de netto
lading Qingesloten (binnen dat oppervlak
met ε 0 = 8,55 *10-12 C²/N*m²
Qingesloten: nettolading volledig ingesloten door oppervlak
Opm: een lading buiten het oppervlak kan een invloed hebben op de positie van de
elektrische veldlijnen, maar niet op het netto aantal lijnen dat het opp
binnenkomt/verlaat
Opm: WVG is veel algemener dan de WVC, deze is geldig voor elk willekeurig elektrisch
veld (nt enkel statische elektrische ladingen)
Het verschil tussen ingaande en uitgaande flux van het elektrisch veld over een
willekeurig gesloten oppervlak is het gevolg van de lading binnen dat oppervlak
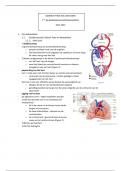
WET VAN COULOMB VOLGT UIT WET VAN GAUSS
1. Wet van Coulomb afleiden uit de wet van Gauss
Stel imaginaire bol met straal r, lading Q in middelpunt symmetrie
o E dezelfde grootte in elk willekeurig punt van dit bolvormig oppervlak
o E radiaal naar buiten/binnen gericht, ⊥ op
opp, // aan dA
o Oppervlakte (A) vd bol met straal r: 4π r²
Wet van Coulomb
2. Wet van Gauss afleiden uit de wet van Coulomb
Stel 1 puntlading A omgeven door een imaginair bolvormig oppervlak
o Coulomb: Elektrisch veld in bolvormig oppervlak: E = (1/4πε)(Q/r²)
Superpositieprincipe:
Opm: Door oppervlak A2 gaan hetzelfde aantal veldlijnen (als gevolg
van lading Q) als door het bolvormig oppervlak A1
Flux ∝ aantal lijnen door opp
Flux A1 = flux A2
2