Samenvatting
samenvatting hoofdstuk 2 - Rijen en reeksen
Een samenvatting van hoofdstuk 2 met de focus op wat geleerd moet worden.
[Meer zien]Voorbeeld 1 van de 3 pagina's
Voorbeeld 1 van de 3 pagina's
In winkelwagengesponsord bericht van onze partner
Gekoppeld boek
Titel boek:
Auteur(s):
- Uitgave:
- ISBN:
- Druk:
Voorbeeld van de inhoud
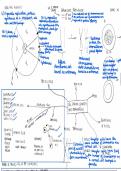
Hoofdstuk 2 rijen, reeksen en iteratieprocessenRijen
Getallen uit een rij worden ook wel termen genoemd. Hierin is de 1e term t1, de 2e t2 en de ne is tn
Een oneindige rij, zoals de naam al zegt loopt van de eerste term tot in de oneindige term: t 1, t2, t3, …,
tn, …
Uit het beginstuk van een rij is niet altijd op te maken hoe deze verder zal vorderen, wel is het te
voorspellen aan de hand van het vinden van patronen in deze rij.
Rijen kunnen meetkundig en rekenkundig zijn
- Meetkundige rijen: termen worden met een constante factor (r: de reden van de
meetkundige rij) vermenigvuldigd
- Rekenkundige rijen: een constant getal wordt afgetrokken/opgeteld bij de termen
Een belangrijk aspect van een oneindige rij is de gedraging in de oneindigheid. Als een rij een limiet
kent, dan is deze convergent het heeft een eindgetal
Anders is deze divergent blijft toenemen/afnemen
Reeksen
Reeks: de termen van een rij bij elkaar opgeteld oftewel de som van de termen.
Een reeks vormt ook een rij van de som van eerste n termen, hierbij is S 2 dus de som van de 1e en 2e
term en S3 is de som van de 1e, 2e en 3e term en Sn dus van de 1e, 2e , …, ne
Omdat een reeks ook een rij van termen is en dus een limiet kan hebben, kunnen ook reeksen
convergent of divergent zijn.
- Partiële som: de som van de beginterm tot en met de term t n
Een meetkundige reeks wordt verkregen door de termen van een meetkundige rij bij elkaar op te
tellen. De partiële som van deze reeks is eenvoudig te bereken door de algemene formule:
1−r n
Sn=a
1−r
Meetkundige reeksen zijn convergent als geldt:
-1 < r <1
Hierbij benadert rn 0 naarmate n oneindig wordt. Invullen in de algemene formule voor S n geeft:
1−r n a
S= lim S n=lim a =
n→ ∞ n→∞ 1−r 1−r
Voordelen van het kopen van samenvattingen bij Stuvia op een rij:
Verzekerd van kwaliteit door reviews
Stuvia-klanten hebben meer dan 700.000 samenvattingen beoordeeld. Zo weet je zeker dat je de beste documenten koopt!
Snel en makkelijk kopen
Je betaalt supersnel en eenmalig met iDeal, creditcard of Stuvia-tegoed voor de samenvatting. Zonder lidmaatschap.
Focus op de essentie
Samenvattingen worden geschreven voor en door anderen. Daarom zijn de samenvattingen altijd betrouwbaar en actueel. Zo kom je snel tot de kern!
Veelgestelde vragen
Wat krijg ik als ik dit document koop?
Je krijgt een PDF, die direct beschikbaar is na je aankoop. Het gekochte document is altijd, overal en oneindig toegankelijk via je profiel.
Tevredenheidsgarantie: hoe werkt dat?
Onze tevredenheidsgarantie zorgt ervoor dat je altijd een studiedocument vindt dat goed bij je past. Je vult een formulier in en onze klantenservice regelt de rest.
Van wie koop ik deze samenvatting?
Stuvia is een marktplaats, je koop dit document dus niet van ons, maar van verkoper timodiederik. Stuvia faciliteert de betaling aan de verkoper.
Zit ik meteen vast aan een abonnement?
Nee, je koopt alleen deze samenvatting voor €2,99. Je zit daarna nergens aan vast.
Is Stuvia te vertrouwen?
4,6 sterren op Google & Trustpilot (+1000 reviews)
Afgelopen 30 dagen zijn er 70055 samenvattingen verkocht
Opgericht in 2010, al 14 jaar dé plek om samenvattingen te kopen