Samenvatting Rekenen met hele getallen

Hoofdstuk 1 | Hoofdrekenen in groep 5 – 8
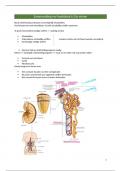
Wat is hoofdreken?
Handig en flexibel rekenen op basis van bekende getalrelaties en rekeneigenschappen.
Hoofdrekenen is rekenen met het hoofd, kladpapier toegestaan.
- Getalrelaties: positie in telrij (positionering), structuren binnen getallen (ontbinden,
splitsen, samenstelen) en relaties tussen getallen, analogieën (overeenkomst) en
steunsommen gebruiken.
- Rekeneigenschappen:
o Wisseleigenschap communicatieve eigenschap: 12+30 = 30+12
o Verdeeleigenschap distributieve eigenschap: 13x6 = 10x6 + 3x6
o Inverse relatie optellen / aftrekken en vermenigvuldigen / delen




3 vormen van hoofdreken bij + en –
1. Rijgend hoofdrekenen
- Het 1e getal blijft heel, het 2e getal wordt er in delen aan toegevoegd of afgehaald.
- Model: lege getallenlijn

2. Splitsend hoofdrekenen
- Getallen worden gesplitst in 100-, 10- en eenheden -> afzonderlijk bij of van elkaar.
- Splitsend: 36 + 28 = 30 + 20 en 6 + 8
- Splitsend aftrekken met tekorthandeling: 36 – 28
30 – 20 = 10 6 – 8 = 2 tekort -> 10 – 2
- Splitsend met optelhandeling: 36 – 28
30 – 20 = 10 10 + 6 = 16 16 – 8 = 8
3. Gevarieerd hoofdrekenen; varia
- Varia-aanpak compenseren
75 – 48 =
75 – 50 = 25
2 teveel afgehaald -> 25 + 2 = 27
56 + 39 =
56 + 40 = 96
1 extra -> 96 – 1 = 95
- Varia-aanpak transformeren
68 – 29 = 69 – 30
56 + 39 = 55 + 40
o Tribunecontext

, - Varia-aanpak aanvullen; alleen bij aftrekken
62 – 59 =
o Hoeveel erbij om op 62 uit te komen?
o Bijna-verdwijnsom
- Varia-aanpak inverse relatie; alleen bij aftrekken
60 – 45 = 15 want 15 + 45 = 60
Let op:
- Verschillende strategieën -> kies de handigste oplossingsmanier voor een bepaalde
opgave.
- Opbouw staat vast: rijgen -> splitsen -> varia.

3 vormen van hoofdrekenen bij x en :
195 : 5 =
Rijgaanpak Splitsaanpak Varia aanpak
Compenseren Transformeren
Opvermenigvuldigen 150 : 5 = 30 200 : 5 = 40 195 : 5 =
10 x 5 = 50 45 : 5 = 9 5 te veel -> dus 1 te 390 : 10 = 39
20 x 5 = 100 195 : 5 = 39 veel: 40 – 1 = 39
30 x 5 = 150
9 x 5 = 45
39 x 5 = 195


Handig rekenen met nullen
- Vermenigvuldigen: nullen weghalen -> later toevoegen bij het antwoord
12.000 x 600 =
12.000 : 1000 en 600 : 100
12 x 6 = 72
72 x 1000 x 100 = 7.200.000
Begrijpen kinderen dit? Nullen weghalen en terugplaatsen
- Delen: nullen schrappen
2.000.000 : 40.000 = :1000
2.000 : 40 = : 10
200 : 4 = 50
1.

, Hoofdstuk 4 | Tafels in groep 4 - 5
4.1 Rekenen in de basisschool van Walt Disney
1 2 3 4 5 6 7 10
Een Twee Drie Vier Vijf Zes Zeven Een-nul
1 greep en nul vingers
9 10 11 12 13 14 15 16
Een- Een- Een- Een- Een-vijf Een-zes Een-zeven Twee-nul
een twee drie vier
Twee-vijf = 2 x 8 + 5 = 21
Een-nul Twee-nul Drie-nul Vier-nul Vijf-nul Zes-nul Zeven-nul Een-nul-nul


4.1.1 Zelf aan de slag
1. Telrij opzeggen en tellen om het aantal vast te stellen
2. Verkort tellen
3. Gestructureerd tellen (tafels van vermenigvuldigen)
4.1.2 Reflectie
1. Opschrijven van de telrij uit het land van Walt Disney
1 2 3 4 5 6 7 10
11 12 13 14 15 16 17 20
21 22 23 24 25 26 27 30
2. Opzeggen van de telrij uit het land van Walt Disney
Schrijfwijze en uitspraak komt overeen met de wijze van uitspreken van getallen. Onze
manier van uitspreken en opschrijven is niet gelijk -> verwarring.
3. Aantal bepalen in het land van Walt Disney
Vakken van 10 bij 10 (dus 100) te tellen = 8x8
4. De tafel van 4, 7 en 5 uit het land van Walt Disney
De tafel van 7
De tafel van 4 1x7 7 Omkering van
1x4 4 Lijkt op de tafel 2x7 16 de
2x4 10 van 5 in het 3x7 25 antwoorden
3x4 14 tientallenstelse 4x7 34 (2x7 = 16, 7x7
4x4 20 l 5x7 43 = 61).
5x4 24 6x7 52 Optelling van
6x4 30 7x7 61 de 2 cijfers
7x4 34 10 x 7 70 steeds 7 (ook
10 x 4 40 bij tafel van
9).
De tafel van 5
1x5 5 Uitrekenen = gebruik
2x5 12 maken van sommen
3x5 17 die je al kende of
4x5 24 verwisseleigenschap
5x5 31 , halveren, een keer
6x5 36 meer / een keer
7x5 43 minder.
10 x 5 50