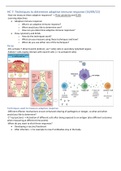
,A echelon form
system of the
is matrix has
consisenting row
an no
the
gorn
:
of
10 ..... 06
· where b + 0
A thus consisent in case has least solution
system is it at one
·
, .
o
unique
solution When there are variables Otherwise infinite
no
gree ,
amount solutions
of
Vectors
A matrix with just one column is called a rector
m= (3) ,
v =
(2)
Note that n + U
.
The complete
Jet vectors with two entrice is denoted by R
of "
, rectors
With three entries
by ,
and rectors With n entrie by R!
=)
Definitions
Let h and v be vectors in A :
= no v .
Their u
n + v is then defined a : n + v =
W
Definition :
Let
h be a vector in R and let Ch be a salar .
Then , the
(en)
ecalar multiplication with
of
> h is given by :
2 =
The o vector ,
is a vector whose entries are all
equal
to 0
.
Then , the
following propertie hold for all vectore U, v
,
WER and
= calcr <, d = k + v = V +4
·
(u + v) +w = n + (V + w)
· uto = 0 +u = u
4 + u
( 4)
-
· n + -
= =
0
,·
c(u+ u) = cu + 2r
·
(( + d)u = Eu + du
·
<(du) = (d) v
·
In = u
Given are the rectors v
,, We
, ...,
Un &V and Scalers C
,, 12 , ..., In
.
Y =
C , Vi + C2Ve +.... + CUn
is called a linear combination
of u
, ....,
Un with
treights < ,
...,
<
Span
If then the all lineur combination
"
V
,
...
un are in ,
cet of of
V
, ..., Un
is denoted
by Span &U, .....) Vul and termed the subset
of B
spained by V
1
, ... m
Thus :
SpanEU
, ..... rub = 2, v , + Seve +.... + CrVK
Span(s) =
[ civ : 1 vies]
The recrorb is in spanEU ,, Ve , ...,
U. 3
if : X, V , +
X2 Vn +... + X - Un = b
has a solution .
Thus the zero , rector is always in the span
.
Span 327 hae a line through the origin .
Spand U
,, Wz3 is a plane through the origin
Matrices and rectors
#f A is a mx n matrix ,
and B is a 1x matrix , then product C= AB
is an MXr matrix
. The (i)j) entry of a product is computed an
follows :
Cij = Giz bij + diz bizj + - ... + Gin
buj.
Let A be an Mx1 matrix
. Then , the following statements are
either all true or all false :
& For each b in
M
the equation Ax = b has a volution
,
& Each b in Ah is linear combination of the columns
a
ofA
② The column of
A opan Ru
& A has a pivot position in
every row
.
, Werke 2:
Homogeneous lineur systems
Homogeneous if it can be written an Ax = 0 where o is the zero rector
,
in B
Theorem :
For a
homogenous system with evariables and linear equations , there are
infinitely maysolutions ig m =1
Thus ,
in case there is at least one
free variable ,
then the cyclem
has infinitely many solutions .
#f X1 = -
X g
,
Xz = X 3 and X 3 is
free
The general of Ax = o has the vector solution :
X =
() [) =
=
= (i)
Thus X = X3 v
(di& S () (0) x(i)
X, = 3 -
xy
+
= 1 + xxx
= =
x = -
O O g Xs is free
The X =
p + X 3
Linear independente
Definition :
A V Un linearly independent inf the colution
setogrectors Va Vz is
"
,, , < ,
to the
vector equation X , V1 + X Vz +... + XeUn = 0
hue X1 X2 o solution
Only Xn = as a
, , ....,
Thurs ,
we can also make the definition for linear dependence :
Definition :
A get
of Vector
v
, Ve , ...,
Un is
linearly dependent if there are
Backers XI < +1 ,
-
, with at least one salar not zero ,
such that :
X vi + X2Vz + -. . + Xn Un = 0
system of the
is matrix has
consisenting row
an no
the
gorn
:
of
10 ..... 06
· where b + 0
A thus consisent in case has least solution
system is it at one
·
, .
o
unique
solution When there are variables Otherwise infinite
no
gree ,
amount solutions
of
Vectors
A matrix with just one column is called a rector
m= (3) ,
v =
(2)
Note that n + U
.
The complete
Jet vectors with two entrice is denoted by R
of "
, rectors
With three entries
by ,
and rectors With n entrie by R!
=)
Definitions
Let h and v be vectors in A :
= no v .
Their u
n + v is then defined a : n + v =
W
Definition :
Let
h be a vector in R and let Ch be a salar .
Then , the
(en)
ecalar multiplication with
of
> h is given by :
2 =
The o vector ,
is a vector whose entries are all
equal
to 0
.
Then , the
following propertie hold for all vectore U, v
,
WER and
= calcr <, d = k + v = V +4
·
(u + v) +w = n + (V + w)
· uto = 0 +u = u
4 + u
( 4)
-
· n + -
= =
0
,·
c(u+ u) = cu + 2r
·
(( + d)u = Eu + du
·
<(du) = (d) v
·
In = u
Given are the rectors v
,, We
, ...,
Un &V and Scalers C
,, 12 , ..., In
.
Y =
C , Vi + C2Ve +.... + CUn
is called a linear combination
of u
, ....,
Un with
treights < ,
...,
<
Span
If then the all lineur combination
"
V
,
...
un are in ,
cet of of
V
, ..., Un
is denoted
by Span &U, .....) Vul and termed the subset
of B
spained by V
1
, ... m
Thus :
SpanEU
, ..... rub = 2, v , + Seve +.... + CrVK
Span(s) =
[ civ : 1 vies]
The recrorb is in spanEU ,, Ve , ...,
U. 3
if : X, V , +
X2 Vn +... + X - Un = b
has a solution .
Thus the zero , rector is always in the span
.
Span 327 hae a line through the origin .
Spand U
,, Wz3 is a plane through the origin
Matrices and rectors
#f A is a mx n matrix ,
and B is a 1x matrix , then product C= AB
is an MXr matrix
. The (i)j) entry of a product is computed an
follows :
Cij = Giz bij + diz bizj + - ... + Gin
buj.
Let A be an Mx1 matrix
. Then , the following statements are
either all true or all false :
& For each b in
M
the equation Ax = b has a volution
,
& Each b in Ah is linear combination of the columns
a
ofA
② The column of
A opan Ru
& A has a pivot position in
every row
.
, Werke 2:
Homogeneous lineur systems
Homogeneous if it can be written an Ax = 0 where o is the zero rector
,
in B
Theorem :
For a
homogenous system with evariables and linear equations , there are
infinitely maysolutions ig m =1
Thus ,
in case there is at least one
free variable ,
then the cyclem
has infinitely many solutions .
#f X1 = -
X g
,
Xz = X 3 and X 3 is
free
The general of Ax = o has the vector solution :
X =
() [) =
=
= (i)
Thus X = X3 v
(di& S () (0) x(i)
X, = 3 -
xy
+
= 1 + xxx
= =
x = -
O O g Xs is free
The X =
p + X 3
Linear independente
Definition :
A V Un linearly independent inf the colution
setogrectors Va Vz is
"
,, , < ,
to the
vector equation X , V1 + X Vz +... + XeUn = 0
hue X1 X2 o solution
Only Xn = as a
, , ....,
Thurs ,
we can also make the definition for linear dependence :
Definition :
A get
of Vector
v
, Ve , ...,
Un is
linearly dependent if there are
Backers XI < +1 ,
-
, with at least one salar not zero ,
such that :
X vi + X2Vz + -. . + Xn Un = 0