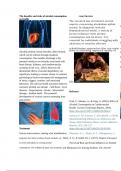
RELATIVISTISCHE KINEMATIK
Galilei Transformation t =
t Lorentz Transformation ct' =
p (ct -
BX) with B= v
=
x =
x -
vt x =
y(x
-
B(t)
mit invarianten :
mit invarianten :
En (tnim) ,
Ez(tz ,2) (AS) =
c
=
(At) 2 -
(xx) -
(xy) -
(xz)
im MINKOWSKI-RAUM :
Lorentz-Vektoren : x" = (t , ) =
(x x , ,
x2 ,
xx) contravariant X =
garx
Xm = ( , -*) =
(X0 ,
X1 ,
42 ,
xa) covariant -Xa =
garX
1
S
( e S =
O S 0
gilt
:
Es
Eu
Metrik : · mit Summations-Konvention :
... I
zeitartig
ur
gMugge
= M >
(MinKorski)
G ggru
O
p -
1
=
gergru x2 -
To
8
Lichtartig
raumartig
( bedeutet nicht
gar
=
gru
~
=
invariant unter
Skalarprodukt :
X -
y
=
gMX ym
=
x
ya
=
gaxy =
XeY Lorentz-Transformationen
Lorentz -Transformation :
Lineare Transformation von einem
Bezugssystem ins andere , wobei der Abstand zweier
N I I' und Raumzeit
Ereignisse in de 4-dim invariant ist
: --
X y .
.
↑
bewegt sich mit v
relativ zu I
X -
Xm = Xv wobei
=X und xy
=
Xy = =
g
xm ->
ym) =
NXv Länge" bleibt erhalten Metrik bleibt erhalten
B Boost in
.
X-Richtung
z .
:
!
( Bu
1 1
eigentliche Lorenztransformation"
=
U up =>
det 1 det 1 =+
keine Raumspiegelungen
-
=
o wenn
1 =
18 = 0 Orthochrone Lorenztransformation" >
Kein VE-Wechsel for !
den
Gruppe die BOOSTS und ROTATIONEN
enthält ,
z B
. .
Rotation im 3D-Raum
P'(x) &(x)
I
D(x)
(0
1000 Skalarfeld >
- =
An R Au(x (x)
Am() Am') XmAr(x)
=
vertorfeld + =
oder :
An(x) =
+ =
Am(x) + 0x drAm(x)
Ableitungen : da == ( 5) =
D'Alembert
Operator OMOM =
-
A =
I in der Poincare-Gruppe :
Star
,
Geschwindigkeit Un : =A gemessen (4) mit uMUm =
ch Mit Konstantem 4-vektor am
Impuls ph MoUn : = =
(E , p) =
(po p) ,
=
MoU(c 4) ,
mit popu =
Moc
ENERGIE-IMPULS-BEZIEHUNG nach
entwickelt
↓
~
nicht-relativistisch : Im :+ = m + (
aus
p
==
Er-p2 =
m2 =
Er =
mi +
↑
wenn Teilchen
(non-shell")
auf
sonst :
Massen-Schale
Virtuell !
E = mac" + ErcGat1 L Ultra-relativistisch :
1pkm :
E
L
,
Impulserhaltung : Bei Reaktionen a+ b +
C+ d +... am Teilchen
beschleuniger ist die Summe der Vierer-impulse erhalten .
Es
gilt also (bei n Teilchen im Endzustand) P2 Po +
Pu
+...
p pr
:
.
+ =
/ EntEr Est En
-
a
B
Pa Pu
=
z . 7
perpe
+ =
&
. =
b
7
p +
52 =
53 +
54
Zweikörperzerfall +
(Ma 5) po pc (Eb Po 5)
B pa po Pc par Es Ma Eb Es
=
mit + +
= + =
.
z
= = = +
. , ,
b
as - =
b =
-
5 ma-M
27
=>
EB-ms = Ec -
Mc
-
-
> Es =M-Mc und E
=
2 Ma
, STREUTHEORIE
-
7
Teilchendichte Anzahl Teilchen F d
Na im
Target Nb no
=> = .
Teilchenstrahl a
7
(innerhalb Strahlgverschnitt)
-
Teilchendichte Ma =
Na/V
+ -
Va
2
-0
& 00
VatFaAnzahlanTeilchen (
&
2 durc
Strahl-
Teilchenfluss ja Nava =
Target b =
fläche Strahlfäche
. Zeit
↓
geometrischer
Wirkungsquerschnitt Luminosität L =
ja .
No =
Anzahl
#
Teilchenbegegnungen
äche .
Zeit
[is]
Or
GrößedesTarget [m]
Reaktionsrate R =
ja Nb
.
Ob
=
Los =
nzanzgegegnungen
Zeit
[5]
7
Differentieller
Wirkungsquerschnitt
(proRaumwinkelelement
=
↳
mit n bunches
a + b +
c + d
MANDELSTAMM
EsI mia
[
<
(1) Ea"-IPal VARIABLES
Da Ma
= = :
1
Einheit barn" ( &
9 (1) 43" Es-1Pok My2
=
=
bunch
[1 barn] =
10-2"cme Tläche F
EaED-PaPb
-
#) Paps
=
=
pb = 10-1 barn
10-15
fb barn
#Spar-por lEatEsT-IP
=> = =
+
Center-of-Mass-Frame (COM)
⑫
lis
b
(Lab)
a
If
Target rest
frame
0 -
> >
- .
et
- ⑨
--- a 53 (pa) (f)
dh 5 (b) ↓ beschien
He
= -
= = =
.
(EatE S
frei bei
(
↓
t D frei
bei
-
-
Da Ds
t
par
+
= => + = +
z
( /Ea
(Pa-pot
par
=
(5) b
pa =
=
↳
übergangsmatrix :
for
(E)
:
(5)
=
a
>
- V M
IME PD2
=
=
Mei =
(flltli) =
< 4f / Hinz 14:]
s (pa py) pa po 2papy
=>
=
+
=
+ +
vorhanden
=
Ma + Mb2 +
ZEaMb mit 5 = Eac + Ega ↓ Energie
für Endzustand
Reaktions
rate
-
Wi = IMROCEf) mit dE =
vdp
=
zVE2 für MapE
-
Transformations :
(a) =
(pr- *) (5) v( ) =
mit Zustandsdichte O(E) =Es
= Dichte an Zuständen mit der Energie El
und (5) (pre) (m) = =
v ( -ma
i
~
RULE
mit
=E ) ta E -
Lösungen (freie Schrödingergleichung) :
ELASTISCHE STREJUNG an einem Potential
Ef
Tik) = Epix = Fazit gip
Pi -) Ye) = ipt = gift zipf
> U(r)
Tilt-Zerübergangsmatrix element :
First
Yfr) = gipr
Tri < Yf/FintI4i) =
-
JdBr Yfr) U(r) 4 : (F)
M
= -
mit =
Pi -
Pf Yukawa Potenzial mit 1111
=
- der ei U(r)
=>
Fouriertransformierte des Potentials
m Marget =>
(pi) =
15f) =
p
=
mial =>
Ig) =
2/pi) sin
Far Former
- 7
=>
Betragsquadrat der Streuamplitude mit = =
Pf
>
mit Et Ph M = dp
&
für punktförmige Ladung F(g) 1
=
Coulomb-Wechselwirkung
insinE
E
FEYNMANN- 1 -
und schwere Teilchen mmtarget
q pi Df
-
=
DIAGRAMM -
Z Propagator und nicht-relativistisch Erin
=
to
=
Strahl
target
-
Wechselwirkung Schwache-Wechselwirkung
Son Z
im Atomkene
↳ starke-Wechselwirkung Rutherford-
=> Streuquerschnitt
·
.
Sie
8
i
↓ Streuquerschnitt
Punktladung
-
einer