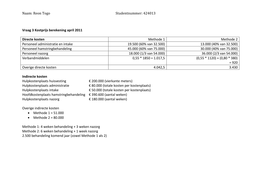
Blok 3: analyse van categoriale data
Gebruikelijke analyse van categoriale gegevens:
Starten met beschrijvende statistieken (frequentie- en kruistabellen):
- Absolute frequenties
- Relatieve frequenties
- Eventueel visueel
Of verklarende statistieken – effectmaten:
- Relatief risico
- Odds ratio
- In de basis alleen bruikbaar in 2x2 situaties
Weergave van effecten is niet mogelijk met een beschrijvende tabel, hiervoor moet je percentages
toevoegen waarna je uiteindelijk gaat rekenen met contrasten/effectmaten.
Als je in 1 tabel meerdere RR’s of OR’s met de bijbehorende BI’s gaat bepalen is dat inefficiënt en
veel werk, ook zorgt het voor alfa inflatie als bij t-toetsen (type 1 fout maken).
Daarnaast is het inefficient omdat je maar een deel van de hele steekproef uit een hele tabel gebruikt
en je hebt veel meet contrasten om te bekijken.
Hoe los je dit op? chi-kwadraattoets voor categoriale gegevens
Waarbij weer een H0 geldt als geen verband, en een H1 als wel verband. Lijkt op de ANOVA je
berekent of er überhaupt een verband is, maar je weet niet waar of hoe de richting precies zit.
Voorbeeld chi-kwadraattoets
Verwachting (onder de H0) binnen elke behandeling dezelfde verhouding (non-)responses. Want
H0 = geen verband tussen behandeling en depressie.
Optie 1 een H0 bij categoriale gegevens zelf invullen in een tabel:
1. Kijk naar de randtotalen hoevaak responsen voorkomen
2. Hoeveel mensen (absoluut aantal) verwacht je in elke cel (bijv. 60,1% van 79)
3. Ingevulde cellen zijn dan de populatieverwachtingen
4. Dit doe je omdat je verwacht dat in elk vakje de respons hetzelfde zou zijn gegeven de
randtotalen van een steekproef als de H0 waar is, dan zou er geen verschil in effect zijn.
Optie 2 verwachte frequenties bij H0 invullen in tabel:
1. Randtotalen x aantal observaties
minder inuitief maar is sneller.
, Optie 3 verwachte frequenties in SPSS:
Crosstabs > cells > expected counts
Uiteindelijke beschikbare gegevens voor berekenen:
1. Verwachting onder de nulhypothese
2. Geobserveerde data
Hoe sterk verschilt het om te veronderstellen dat de H0 niet waar is? Dit kan je doen middels de chi-
kwadraat!
Chi-kwadraattoets:
Zijn die verschillen groter dan wat we o.b.v. toeval zouden verwachten?
Uitleg:
- Voor élke cel wordt bovenstaande formule uitgevoerd
- Sigma; som x aantal keer herhalen voor aantal groepen die je hebt
- In dit voorbeeld zou het 9 zijn 3x3 cellen
- G zou hier staan voor CEL
- Som tel je bij elkaar op resultaat chi-kwadraat grootheid
Formule kort gezegd: observer-expexted van een bepaalde groep, in het kwadraat, gedeeld door de
verwachting, voor alle cellen. Opgeteld = resultaat.
Ingevuld in voorbeeldopdracht
2
Gebruikelijke analyse van categoriale gegevens:
Starten met beschrijvende statistieken (frequentie- en kruistabellen):
- Absolute frequenties
- Relatieve frequenties
- Eventueel visueel
Of verklarende statistieken – effectmaten:
- Relatief risico
- Odds ratio
- In de basis alleen bruikbaar in 2x2 situaties
Weergave van effecten is niet mogelijk met een beschrijvende tabel, hiervoor moet je percentages
toevoegen waarna je uiteindelijk gaat rekenen met contrasten/effectmaten.
Als je in 1 tabel meerdere RR’s of OR’s met de bijbehorende BI’s gaat bepalen is dat inefficiënt en
veel werk, ook zorgt het voor alfa inflatie als bij t-toetsen (type 1 fout maken).
Daarnaast is het inefficient omdat je maar een deel van de hele steekproef uit een hele tabel gebruikt
en je hebt veel meet contrasten om te bekijken.
Hoe los je dit op? chi-kwadraattoets voor categoriale gegevens
Waarbij weer een H0 geldt als geen verband, en een H1 als wel verband. Lijkt op de ANOVA je
berekent of er überhaupt een verband is, maar je weet niet waar of hoe de richting precies zit.
Voorbeeld chi-kwadraattoets
Verwachting (onder de H0) binnen elke behandeling dezelfde verhouding (non-)responses. Want
H0 = geen verband tussen behandeling en depressie.
Optie 1 een H0 bij categoriale gegevens zelf invullen in een tabel:
1. Kijk naar de randtotalen hoevaak responsen voorkomen
2. Hoeveel mensen (absoluut aantal) verwacht je in elke cel (bijv. 60,1% van 79)
3. Ingevulde cellen zijn dan de populatieverwachtingen
4. Dit doe je omdat je verwacht dat in elk vakje de respons hetzelfde zou zijn gegeven de
randtotalen van een steekproef als de H0 waar is, dan zou er geen verschil in effect zijn.
Optie 2 verwachte frequenties bij H0 invullen in tabel:
1. Randtotalen x aantal observaties
minder inuitief maar is sneller.
, Optie 3 verwachte frequenties in SPSS:
Crosstabs > cells > expected counts
Uiteindelijke beschikbare gegevens voor berekenen:
1. Verwachting onder de nulhypothese
2. Geobserveerde data
Hoe sterk verschilt het om te veronderstellen dat de H0 niet waar is? Dit kan je doen middels de chi-
kwadraat!
Chi-kwadraattoets:
Zijn die verschillen groter dan wat we o.b.v. toeval zouden verwachten?
Uitleg:
- Voor élke cel wordt bovenstaande formule uitgevoerd
- Sigma; som x aantal keer herhalen voor aantal groepen die je hebt
- In dit voorbeeld zou het 9 zijn 3x3 cellen
- G zou hier staan voor CEL
- Som tel je bij elkaar op resultaat chi-kwadraat grootheid
Formule kort gezegd: observer-expexted van een bepaalde groep, in het kwadraat, gedeeld door de
verwachting, voor alle cellen. Opgeteld = resultaat.
Ingevuld in voorbeeldopdracht
2