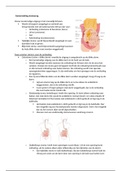
Matemáticas

MATEMÁTICAS
I

,IEIYAI :(ÓNICASY (UÁDR
-




÷.mm
Las
CÓNICAS importan
cónicas más


elipses e hipérbolas son


DEGENERADAS . El resto so




Se define como :




'
axl +
by +
cxy + dx + f. = O
ey +




PARÁBOLA



[aso1:q=k DCP F) =D CP ,
,
recta directriz )



Fiyi

µ
=
y +
L
Elevando al cuadrado :




y.yyyg.gg ya g. , + ↳y →




Foco
( o /
÷)


Caso 2 : ✗ =
ky
'




K> o abierta ha
OX vértice ( 0,0 )
kco abierta ha

,ELIPSE




Ecuación reducida :

÷ 4¥ + = 1 a




* Como A está en la elipse :




d (A) F) 1- d ( A
,




/ a- f) + la f) + = K




* Como B está en la eli

Ld (B. F) = 2a → d CB ,

"


'
'
b
f = ar -




Pcx está la
,
y)
en
elipse , por tanto
:




lx-ifj-yf-ifx-fj.ly#=2al(xi-fT-TT=(2a-Fg-yY
desarrollando y simplificando :




✗
f- al = - a
Ég ÷ ¥- +




* Si a = b → se trata de una circunferencia de centro (op )
a

, signo contrario



&÷
2
✗

* si a > b →
-
+ = 1 f- = á -
b
ai


centro ( 0,0)
vértices ( a , o) , f- a , o) ,
( o , b) , 10 ,
-
b)
f
a > b :
focos ( f ,
o ) ,
( fi
-



e =


ób má
b) a :
focos ( o , f) , (o ,
f)
-
a




HIPÉRBOLAS

CASOF Ecuación reducida :
÷ ÷ -




distancia entre focos f
l =

a
-
=



distancia entre vértices



ya
€2
-
Ecuación reducida :

J
-




distancia entre focos
e =




distancia entre vértices
=

÷

ECUACIÓN REDUCIDA DE UNA CÓNICA




• Si C =/ O → girada

•
Si c. = o → no girada


CÓNICAS TRASLADADAS → C = O



'
AXZ +
by + dx f--0
+
ey +