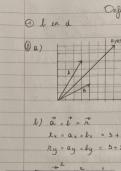H6: De steekproevenverdeling
1 Steekproevenverdeling van het gemiddelde
1.1 Eigenschappen
- E ( X ) =μ X
σ 2X
- V ( X )=
n
1.2 Vorm bepalen
2
σX
- Als X N ( μ X , σ 2X ) → X N (μ X , )
n
- Als n ≥ 3 0
2 Steekproevenverdeling van de variantie
2.1 Eigenschappen
2 n−1 2
- E ( SN X ) = σ
n X
- E ( S2X ) =σ 2X
2.2 Vorm bepalen
2 (n−1)S 2X
- Indien N ( μ X , σ X ) → 2
χ 2n−1
σ X
3 Extra: standaardiseren
2
X N ( μ X , σ 2X ) σX
X N (μ X , )
n
1) Is X normaal verdeeld? 1) Is X normaal verdeeld?
→ gegeven in de opgave σ
2
→ X N ( μ X , σ ) → X N (μ X , X )
2
X
n
→ n ≥3 0
2) Bepalen E ( X ) en V( X ) 2) Bepalen E ( X ) en V( X )
→ E ( X )=μ X → E ( X )=μ X
→ V ( X )=σ 2X → V( X )=¿ σ 2X /n
3) Standaardiseren 3) Standaardiseren
X −μ X X −E ( X ) X−μ X X−μ X
→ Z= → Z= = =
σX √V ( X ) √ σ 2X / n σ X / √ n
1 Steekproevenverdeling van het gemiddelde
1.1 Eigenschappen
- E ( X ) =μ X
σ 2X
- V ( X )=
n
1.2 Vorm bepalen
2
σX
- Als X N ( μ X , σ 2X ) → X N (μ X , )
n
- Als n ≥ 3 0
2 Steekproevenverdeling van de variantie
2.1 Eigenschappen
2 n−1 2
- E ( SN X ) = σ
n X
- E ( S2X ) =σ 2X
2.2 Vorm bepalen
2 (n−1)S 2X
- Indien N ( μ X , σ X ) → 2
χ 2n−1
σ X
3 Extra: standaardiseren
2
X N ( μ X , σ 2X ) σX
X N (μ X , )
n
1) Is X normaal verdeeld? 1) Is X normaal verdeeld?
→ gegeven in de opgave σ
2
→ X N ( μ X , σ ) → X N (μ X , X )
2
X
n
→ n ≥3 0
2) Bepalen E ( X ) en V( X ) 2) Bepalen E ( X ) en V( X )
→ E ( X )=μ X → E ( X )=μ X
→ V ( X )=σ 2X → V( X )=¿ σ 2X /n
3) Standaardiseren 3) Standaardiseren
X −μ X X −E ( X ) X−μ X X−μ X
→ Z= → Z= = =
σX √V ( X ) √ σ 2X / n σ X / √ n