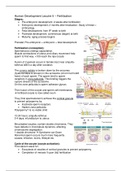
.
61 Volumes
Volume Tr h
Let Plx Plane perpendicular to the X axis
and passing thru thepoint
Area of the intersection of
P x with S
A x
1 DIVIDE a b IN SUBINTERVALS of EQUAL
WIDTH DX WITH ENDPOINTS a Xo X Xny x b
2 CUT S INTO n SLABS BY SLICING S ALONG
THE PLANE Pix
, 3 VOLUME OF 1 SLAB
f dl
DX AXT
h
reima
xi
iÉ DX
Xi t x 5 v him
Dx Alxt
Alx dx
EXAMPLES
1 FIND THE VOLUME OF THE SOLID OBTAINED BY
non BOUNDED by e
y 0 x
1511111 E
4 8
YIFI
re
A x Tr
1 2
Tile
V0 YE e'd T ex tile
, 126 1
VOLUME The dx T ex
2 FIND THE VOLUME OF THE SOLID OBTAINED BY ROTATING THE
REGION BOUNDED BYTHE CURVES y X3 y x 0 ABOUTTHE
x axis
y
Alx TLV TL V2
TL x TL
F x2 x
o
VOLUME A x dx
Tex
6 dx
It
, ROTATING AROUND
Y AXIS
y
Aly dy
91g
Aly
EXAMPLES
FIND THE VOLUME OF THE SOLID GENERATED BY ROTATING
THEREIGON BOUND BY THE CURVES Y X2 X 0 y 4
ABOUT THE Y AXIS
Aly Tly 2
y v TC To
y y dy St
o
VOLUME Aly dy
61 Volumes
Volume Tr h
Let Plx Plane perpendicular to the X axis
and passing thru thepoint
Area of the intersection of
P x with S
A x
1 DIVIDE a b IN SUBINTERVALS of EQUAL
WIDTH DX WITH ENDPOINTS a Xo X Xny x b
2 CUT S INTO n SLABS BY SLICING S ALONG
THE PLANE Pix
, 3 VOLUME OF 1 SLAB
f dl
DX AXT
h
reima
xi
iÉ DX
Xi t x 5 v him
Dx Alxt
Alx dx
EXAMPLES
1 FIND THE VOLUME OF THE SOLID OBTAINED BY
non BOUNDED by e
y 0 x
1511111 E
4 8
YIFI
re
A x Tr
1 2
Tile
V0 YE e'd T ex tile
, 126 1
VOLUME The dx T ex
2 FIND THE VOLUME OF THE SOLID OBTAINED BY ROTATING THE
REGION BOUNDED BYTHE CURVES y X3 y x 0 ABOUTTHE
x axis
y
Alx TLV TL V2
TL x TL
F x2 x
o
VOLUME A x dx
Tex
6 dx
It
, ROTATING AROUND
Y AXIS
y
Aly dy
91g
Aly
EXAMPLES
FIND THE VOLUME OF THE SOLID GENERATED BY ROTATING
THEREIGON BOUND BY THE CURVES Y X2 X 0 y 4
ABOUT THE Y AXIS
Aly Tly 2
y v TC To
y y dy St
o
VOLUME Aly dy