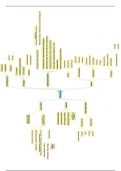
I* DOM VARIABLES
:
!Fe(X) = 0 (2) Fx non-decreasing f (3) E is right-cont .:
fe(x) - i
Density func
- -
b) cythen Fe(x = Fx() lim
aFa(x) Fx(a)
Fe(x) Distribut
=
↑(ac Fe(b) Fe(a) Prob
Fa(x)
x
=
1 x
+ -
=
- .
function
↑(A = a) =
Fa(c) -
4 Fx(a)
↑(A >x) = 1 -
P(Acx) =
1 -
x
- Fx(t) P(A >x) =
1 -
/A ex) =
1 -
Fe(t)
DISCRETE PROBABILITY MODELS DISCRETE EXPECT .
& MOMENTS CONT PROBABILITY MODELS
·
BERNOULLI MODEL -D noves 2
po- EXPECT E( E ) x PP(A =
x) ·
UNIFORM (CONT) -> toti els
=
.
-
·
.
xim
ssibles resultats 1)
intervals amd la meteixa llargada teven
(0 : la mateixa
probabilitat .
G
IP(A 0)
=
1 - p
P(X 1) P 1xb -
a) x + [a b]
baia x(x)
= =
=
,
f((x)
=
=
probability of success)
,
[a
Sp -x 0 x , b]
= Ya
X La
* =
Ha we wile -Be(p) a
acxcb
, x -
FE(x)
b
* ~u([a b))
x ,
· BINOMIAL MODEL-# d'exits en ma
seq, de Berwoullis indes .
· EXPONENTIAL -
per
modelar temps
d'un event
P(A =
k) =
(2)pk qn-
1
n =
0
,
1
....,
d'espera per
l'ocurrencia
,
->
E(E +
1) =
E(X) +
E[4] -
xx
Newt . # ~ Bin (n
p) e[a bAT bE[A) f((x) =
xe 11 a(X)
XE(A)
-
,
a (
E(XE)
=
+
,
B in
+
k
=
(k)p"(1
U
4))"
->
~xx
,
,
y(4 (p
-
-D
E P( n) = (1 1
1 xedt for x30
=
* 1
= +
- =
e
-
E[E 7] ETAJE [1] INDEPDo Fe(x)
= -
=
:
-
.
.
-
!
x
E(7) E(q(A)) , (
Exp(x)
=
*
=
=
· POISSON MODEL - # d'events casuals
que ocurreixen en u tems fixe -
MARKOU-INEG
:
P(Asa)
= El · if En ~Geom() P(*n :
= kn) =
1-11 -
2) "
- xk
Eso
-> 1
e 1 e
-
4)
Pla
=
x k/P(A x)
=
=
Excel
=
MOMENTS -DE[A"]
=
·
· IP(Ast) * > s) =
PP(A)t s) -
* 40(X) (X freq ,
#d'events milja) · k-th central moment of A : · Poison Point Process :
↑(T1H)= IP (*
+? 1)
x
( A)) "P(A (TrExp(X))
-
↳ m) Polnoml E((I E( *))") z(x x) =1
4(Aq 0) 1 e
= -
-
A ~Bin(n
=
=
m
-
quan nom
- =
=
,
x t (r)
constant (x)
convergeix a ma
modelar
· VARIANCE -P second central moment · NORMAL-D pernet nombroses
ferimens naturals socials i
psicologics
,
6 Var(A) El(A E(Al))
=
=
GEOMETRIC
-
MODEL-D # d'intents
=
· L
de Bernoullis per aconseguir el ser exit .
Var( A)
=
E(12) -
E(A)2 fx(x)
1
qk k 1 2 3 Stand Deriv -D 6 == +v Var(A)
N(m 6) = variation)
-
P(E k) (m expect
=
·
p *
=
, , .. .
~
.
= =
(
,
, ,
·
Chebysher Freg -- P(1X- E(X)1a) -
Normal Distrib >N 10 11
·
SUM OF A GEOMETRIC SERIES ~D · Stand . .
-
,
p(k
: En e*
-"
es en e
2
42 4)k
E n) /1
(1
-
(*
=
=
- -
=
=
,
,
agreen estam
P a
=
1 S
1 -
x -
p)↳
( .
H en
· SLIGHT VARIATION
-
# d'intents falliti ar
oMOIURE-LAPLACE :
Binomial tends to a
del der exit : Normal for
large
ser
baws n -
P(E k) qkp k 0 1
(2) par
2
fa(h)
= =
=
a)
, ,
...
P (A
, =
= ~
· LACK OF MEM .
-
I (A ? r+s1A2r) =
P(A3s) ↳Var(A) = 0 -0
A =
E(A)
↳Var(a) 0 · GAMMA -D
procediment acd
Geom(p)
=
a passos
*
~
(a1) a2 Var ( A) cadasom
↳ var indep pren Exp/N quant temps
=
, . de
(A+ )
/t
NEG BiN MODEL-D de ↳ var var(A) +Var(4) +2 Cor(A 7) ↑ (x)
*
t for
en ma
seq
=
=
· . . .
,
at x 0
el # d'intents fins (E 1) Var(1) +Var(I) ~D INDEP
I
indep ↳Var
a- =
Bernoultis
+
,
rribar a (rexits .
↳ var (I) =
E(var(E11)) +
VarIE/IlE)) ↑(x 1)
+
=
xi(x)T(n 1) +
=
n !
xx
(r 1) pqk-r f(x) x - for
-
k=r 1 (M6F) x30
P(A =
h) =
-
,
r +
...
o MOMENT GENERATING FUNCTION =
et (A x) Ganma(x X)
*
r) E (et ) z
NegBin(p
*
*
~
Louk # dintents) MA(t)
=
= =
:
. ,
x= (2)
E(E4)tk ·
Exp Gamma(1 X) Neg Bin cont version
obtenin la distrib
=
2
=
Me(t)
, .
Quen 1
=
grom
· = .
k!
.
k, 0
· BETA-D Euler Beta fus :
· HYPER GEOM . MODEL -
extraiem mos-
/! (1 t)Y
-
tres de tamany'r' d'una pobl .
detanary B(x y) ,
=
t
*
- d+ for x , y 0
inquete im individus de tipus 1 :
(x)T (y)
↑
(n -m) de tipus 2 Volew comptar els +1
B (x
-
y)
=
, T(x +
y)
e est,
(2)(2 z) =
1 2
P(A
=
0
k)
...
= = , ,
(2)
Hypbeom (n
*
~
,
m
,
r)
tots intervali de
· UNIFORM MODEL -D ell
CONT RANDOM VARIABLE
*
~ Beta(x , !
mateixa mateixa
.
la
la long teven prob .
(" ftd probdesie
.
IP(A =
k) =
Yu k = 1
,
2
, . . . ,
·
Fa(x)
=
CONT .
EXPECT .
& MOMENTS
- -
u(n) ETAJ =
E ,
X:
VII) =
x
FTC :
fx(x) =
Fx(x) 0
Expect - E(A) =
(-8xfx(x)dx
oP( A x) = =
Fa(x) -
(Fx(t)
= 0 0 k-th moment- -(A4) =
(x " fa(x) dx
h) central k-th --
E(1 E(X(4) (-8(x- (A)"f((x) =
↑(ac(a
mom
-
.
o
f(a)
+
=
02nd central mom .
is the variance of A :
6 Var(E) (EY)
2
* E
/ E (A)
= =
-
* [A] =
(/z xyf(x y)dxdy ,
:
!Fe(X) = 0 (2) Fx non-decreasing f (3) E is right-cont .:
fe(x) - i
Density func
- -
b) cythen Fe(x = Fx() lim
aFa(x) Fx(a)
Fe(x) Distribut
=
↑(ac Fe(b) Fe(a) Prob
Fa(x)
x
=
1 x
+ -
=
- .
function
↑(A = a) =
Fa(c) -
4 Fx(a)
↑(A >x) = 1 -
P(Acx) =
1 -
x
- Fx(t) P(A >x) =
1 -
/A ex) =
1 -
Fe(t)
DISCRETE PROBABILITY MODELS DISCRETE EXPECT .
& MOMENTS CONT PROBABILITY MODELS
·
BERNOULLI MODEL -D noves 2
po- EXPECT E( E ) x PP(A =
x) ·
UNIFORM (CONT) -> toti els
=
.
-
·
.
xim
ssibles resultats 1)
intervals amd la meteixa llargada teven
(0 : la mateixa
probabilitat .
G
IP(A 0)
=
1 - p
P(X 1) P 1xb -
a) x + [a b]
baia x(x)
= =
=
,
f((x)
=
=
probability of success)
,
[a
Sp -x 0 x , b]
= Ya
X La
* =
Ha we wile -Be(p) a
acxcb
, x -
FE(x)
b
* ~u([a b))
x ,
· BINOMIAL MODEL-# d'exits en ma
seq, de Berwoullis indes .
· EXPONENTIAL -
per
modelar temps
d'un event
P(A =
k) =
(2)pk qn-
1
n =
0
,
1
....,
d'espera per
l'ocurrencia
,
->
E(E +
1) =
E(X) +
E[4] -
xx
Newt . # ~ Bin (n
p) e[a bAT bE[A) f((x) =
xe 11 a(X)
XE(A)
-
,
a (
E(XE)
=
+
,
B in
+
k
=
(k)p"(1
U
4))"
->
~xx
,
,
y(4 (p
-
-D
E P( n) = (1 1
1 xedt for x30
=
* 1
= +
- =
e
-
E[E 7] ETAJE [1] INDEPDo Fe(x)
= -
=
:
-
.
.
-
!
x
E(7) E(q(A)) , (
Exp(x)
=
*
=
=
· POISSON MODEL - # d'events casuals
que ocurreixen en u tems fixe -
MARKOU-INEG
:
P(Asa)
= El · if En ~Geom() P(*n :
= kn) =
1-11 -
2) "
- xk
Eso
-> 1
e 1 e
-
4)
Pla
=
x k/P(A x)
=
=
Excel
=
MOMENTS -DE[A"]
=
·
· IP(Ast) * > s) =
PP(A)t s) -
* 40(X) (X freq ,
#d'events milja) · k-th central moment of A : · Poison Point Process :
↑(T1H)= IP (*
+? 1)
x
( A)) "P(A (TrExp(X))
-
↳ m) Polnoml E((I E( *))") z(x x) =1
4(Aq 0) 1 e
= -
-
A ~Bin(n
=
=
m
-
quan nom
- =
=
,
x t (r)
constant (x)
convergeix a ma
modelar
· VARIANCE -P second central moment · NORMAL-D pernet nombroses
ferimens naturals socials i
psicologics
,
6 Var(A) El(A E(Al))
=
=
GEOMETRIC
-
MODEL-D # d'intents
=
· L
de Bernoullis per aconseguir el ser exit .
Var( A)
=
E(12) -
E(A)2 fx(x)
1
qk k 1 2 3 Stand Deriv -D 6 == +v Var(A)
N(m 6) = variation)
-
P(E k) (m expect
=
·
p *
=
, , .. .
~
.
= =
(
,
, ,
·
Chebysher Freg -- P(1X- E(X)1a) -
Normal Distrib >N 10 11
·
SUM OF A GEOMETRIC SERIES ~D · Stand . .
-
,
p(k
: En e*
-"
es en e
2
42 4)k
E n) /1
(1
-
(*
=
=
- -
=
=
,
,
agreen estam
P a
=
1 S
1 -
x -
p)↳
( .
H en
· SLIGHT VARIATION
-
# d'intents falliti ar
oMOIURE-LAPLACE :
Binomial tends to a
del der exit : Normal for
large
ser
baws n -
P(E k) qkp k 0 1
(2) par
2
fa(h)
= =
=
a)
, ,
...
P (A
, =
= ~
· LACK OF MEM .
-
I (A ? r+s1A2r) =
P(A3s) ↳Var(A) = 0 -0
A =
E(A)
↳Var(a) 0 · GAMMA -D
procediment acd
Geom(p)
=
a passos
*
~
(a1) a2 Var ( A) cadasom
↳ var indep pren Exp/N quant temps
=
, . de
(A+ )
/t
NEG BiN MODEL-D de ↳ var var(A) +Var(4) +2 Cor(A 7) ↑ (x)
*
t for
en ma
seq
=
=
· . . .
,
at x 0
el # d'intents fins (E 1) Var(1) +Var(I) ~D INDEP
I
indep ↳Var
a- =
Bernoultis
+
,
rribar a (rexits .
↳ var (I) =
E(var(E11)) +
VarIE/IlE)) ↑(x 1)
+
=
xi(x)T(n 1) +
=
n !
xx
(r 1) pqk-r f(x) x - for
-
k=r 1 (M6F) x30
P(A =
h) =
-
,
r +
...
o MOMENT GENERATING FUNCTION =
et (A x) Ganma(x X)
*
r) E (et ) z
NegBin(p
*
*
~
Louk # dintents) MA(t)
=
= =
:
. ,
x= (2)
E(E4)tk ·
Exp Gamma(1 X) Neg Bin cont version
obtenin la distrib
=
2
=
Me(t)
, .
Quen 1
=
grom
· = .
k!
.
k, 0
· BETA-D Euler Beta fus :
· HYPER GEOM . MODEL -
extraiem mos-
/! (1 t)Y
-
tres de tamany'r' d'una pobl .
detanary B(x y) ,
=
t
*
- d+ for x , y 0
inquete im individus de tipus 1 :
(x)T (y)
↑
(n -m) de tipus 2 Volew comptar els +1
B (x
-
y)
=
, T(x +
y)
e est,
(2)(2 z) =
1 2
P(A
=
0
k)
...
= = , ,
(2)
Hypbeom (n
*
~
,
m
,
r)
tots intervali de
· UNIFORM MODEL -D ell
CONT RANDOM VARIABLE
*
~ Beta(x , !
mateixa mateixa
.
la
la long teven prob .
(" ftd probdesie
.
IP(A =
k) =
Yu k = 1
,
2
, . . . ,
·
Fa(x)
=
CONT .
EXPECT .
& MOMENTS
- -
u(n) ETAJ =
E ,
X:
VII) =
x
FTC :
fx(x) =
Fx(x) 0
Expect - E(A) =
(-8xfx(x)dx
oP( A x) = =
Fa(x) -
(Fx(t)
= 0 0 k-th moment- -(A4) =
(x " fa(x) dx
h) central k-th --
E(1 E(X(4) (-8(x- (A)"f((x) =
↑(ac(a
mom
-
.
o
f(a)
+
=
02nd central mom .
is the variance of A :
6 Var(E) (EY)
2
* E
/ E (A)
= =
-
* [A] =
(/z xyf(x y)dxdy ,