PROPIEDADES EJEMPLO
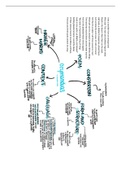
EL DETERMINANTE DE UNA MATRIZ COINCIDE
CON EL DE SU TRASPUESTA
SI UN DETERMINANTE TIENE UNA LÍNEA (FILA O
COLUMNA) DE CEROS,
ENTONCES SU DETERMINANTE ES 0.
SI PERMUTAMOS DOS LÍNEAS DE UNA MATRIZ,
SU DETERMINANTE CAMBIA DE SIGNO
https://marielmatesblog.wordpress.com/
SI UNA MATRIZ TIENE DOS LÍNEAS IGUALES,
SU DETERMINANTE ES 0
SI MULTIPLICAMOS CADA ELEMENTO DE UNA
LÍNEA DE UNA MATRIZ POR UN NÚMERO,
EL DETERMINANTE DE ESA MATRIZ QUEDA
MULTIPLICADO POR ESE NÚMERO.
SI UNA MATRIZ TIENE UNA LÍNEA QUE ES
COMBINACIÓN LINEAL DE LAS DEMÁS
PARALELAS,
ENTONCES SU DETERMINANTE ES 0 (Y
RECÍPROCAMENTE)
EL DETERMINANTE DE UNA MATRIZ COINCIDE
CON EL DE SU TRASPUESTA
SI UN DETERMINANTE TIENE UNA LÍNEA (FILA O
COLUMNA) DE CEROS,
ENTONCES SU DETERMINANTE ES 0.
SI PERMUTAMOS DOS LÍNEAS DE UNA MATRIZ,
SU DETERMINANTE CAMBIA DE SIGNO
https://marielmatesblog.wordpress.com/
SI UNA MATRIZ TIENE DOS LÍNEAS IGUALES,
SU DETERMINANTE ES 0
SI MULTIPLICAMOS CADA ELEMENTO DE UNA
LÍNEA DE UNA MATRIZ POR UN NÚMERO,
EL DETERMINANTE DE ESA MATRIZ QUEDA
MULTIPLICADO POR ESE NÚMERO.
SI UNA MATRIZ TIENE UNA LÍNEA QUE ES
COMBINACIÓN LINEAL DE LAS DEMÁS
PARALELAS,
ENTONCES SU DETERMINANTE ES 0 (Y
RECÍPROCAMENTE)