This is a comprehensive pack of notes about grade 9 equations. It teaches about expressions v.s. equations, solving linear equations, inverse operations, equations with mixed operations, equations with variables on both sides, equations with brackets, equations with fractions, and using equations ...
Equations vs. Expressions different
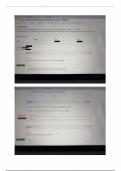
Alarge part of algebra involves expressions and
equations; these are objects
manipulating
and a clear distinction between them is necessary.
EQUATIONS
EXPRESSIONS
What are they?
one
Expressions express a value using Equations are statements that say
value as
variables and constants, e.g. 3x-5. expression must be the same in
another expression. e.g. 3x -5= x.
Acalculation, e.g. "three times a number
then decrease by five", Statements canbe true or false (or always
true or always false) depending on the
value of the variable.
e.g. 3x = 12 or 6 =6 or 3 = 4.
What do they look like?
Expressions do not contain an = sign. Equations contain an = sign.
There is no "other side".
There are two sides, with one expression on
each side.
What is done with them?
e
Expressions are simplified to different Equations are solved (by simplifying the
looking forms that have the same algebraic expressions on either side).
meaning (or value).
Asolution to an equation is a number that
e.g. X +3x has the same meaning as 4x
makes the statement true when it is
does, but they have different forms.
substituted into the variables on both sides.
Expressions are simplified (and cannot be e.g. 4 is a solution to the
solved). statement 3x = 12
because on the left hand side (LHS) we get
avalue of 12,
which is the same as the
Expressions can only be "equal to a value of the RHS.
number" if al the variables have been
substituted for constants, and the
calculation is carried out. Solving an equation means to find
solutions. any/all
e.g. if x is replaced with 3 in the
4x, then the expression will haveexpression
a value of
12 (the "answer after
into 4x is 12). substituting x = 3
Gr.9
, Solving Equations by Inspection
solution(s) by substituting vour answerle)
Solve the following equations by inspection, and check your
separately.
into the LHSand RHS linear.
are
ldentify which of theequations
n+10 = 7 nz n 3
12c =-144 C=- 2
ii.
ii. 2.x =3
3
iv. 12y = -3y
solution)
V. h= 25 (there is more than one
h
vi. p=p(there is more th¡n one solution)
P=I
vi. 2-2* = 32
Operations
Solving LINEAR Equations Using Inverse
Additive and Multiplicative Inverse Operations
gives us the tools to isolate
Many equations are too complicated to solve by inspection, but algebra
a number".
the variable by reducing the equation to a simple statement "the variable eguals
We have seen that to solve an equation means to get the variable on its own on one side of the
equation. To get the variable by itself we need to use inverse operations.
Operation Inverse Operation
IX +
X
X
* Note that powers (exponents) have
special rules
Equations with exponents greater than 1 are NOT(when solving equations).
LINEAR equations.
Gr.9
Unit 8
The benefits of buying summaries with Stuvia:
Guaranteed quality through customer reviews
Stuvia customers have reviewed more than 700,000 summaries. This how you know that you are buying the best documents.
Quick and easy check-out
You can quickly pay through EFT, credit card or Stuvia-credit for the summaries. There is no membership needed.
Focus on what matters
Your fellow students write the study notes themselves, which is why the documents are always reliable and up-to-date. This ensures you quickly get to the core!
Frequently asked questions
What do I get when I buy this document?
You get a PDF, available immediately after your purchase. The purchased document is accessible anytime, anywhere and indefinitely through your profile.
Satisfaction guarantee: how does it work?
Our satisfaction guarantee ensures that you always find a study document that suits you well. You fill out a form, and our customer service team takes care of the rest.
Who am I buying this summary from?
Stuvia is a marketplace, so you are not buying this document from us, but from seller sofiafrenchza. Stuvia facilitates payment to the seller.
Will I be stuck with a subscription?
No, you only buy this summary for R50,00. You're not tied to anything after your purchase.
