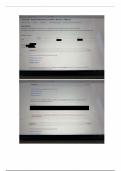
TRANSFORMATIONS
There are different ways of
transforming shapes and Tigures
Translation - moving up, down. left. riaht or a E
these directions. combination o
E
Reflection - mirror images.
E
Line of Reflection
Rotation moving through a given angle around a point. E
Center bf Rototion
E
Translation, reflection and rotation are all known as rigid transformations since the
and size do not change during the figures' shape
transformation (the image is congruent to the original figure)
Dilation - enlargemernt or reduction of a shape from a fixed point. We use the
origin.
enlargemem
original
reduction
Gonter
(origin)
We will study the first two transformations in more detail
to study these transformations by placing the shapes on thenow. We can make it easier
then we can easily see exactly what has happened to theCartesian Plane, because
describe what has happened.
shape and use Maths to
Dilation creates an image which is similar to the original figure
Notation
When we transform a shape, we show that it has
notation'or" . For example, if we transform the shape been
ABCD,
transformed by using the
the new image becomes
A'B'C'D'.
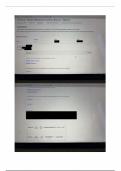
, TRANSLATIONS
B
A
D
D!
B'"
A
Vertical Translations
Horizontal Translations
Fill inthe following:
Fill in the following: - )
3) A(2: 3) ’ A" (24k; -
A( 2:3)’ A'(-6: B(3: 5) ’ B"( 3 i -4)
B'(-S: S)
B( 3 : S) ’
4 ) C(5 i6 ) ’ C"(5;-3)
C(S: 6) ’ C(-3 ;
-3:|) D(Si )’ D"( S ;- &)
D( S: ) - D'(
General change in words:
General change in words:
îransate 8 units lo the le Iranslate units doun
mathematically as: We can write this mathematically as:
We can write this
(xiy)(x-8 ) (xiy) x 4-1 )
horizontal shift: So, in general for any vertical shift:
So, in general for any
(xiy) (X+k : (xiy)(>c
no. of plces qou move
ko left
3 | Page
There are different ways of
transforming shapes and Tigures
Translation - moving up, down. left. riaht or a E
these directions. combination o
E
Reflection - mirror images.
E
Line of Reflection
Rotation moving through a given angle around a point. E
Center bf Rototion
E
Translation, reflection and rotation are all known as rigid transformations since the
and size do not change during the figures' shape
transformation (the image is congruent to the original figure)
Dilation - enlargemernt or reduction of a shape from a fixed point. We use the
origin.
enlargemem
original
reduction
Gonter
(origin)
We will study the first two transformations in more detail
to study these transformations by placing the shapes on thenow. We can make it easier
then we can easily see exactly what has happened to theCartesian Plane, because
describe what has happened.
shape and use Maths to
Dilation creates an image which is similar to the original figure
Notation
When we transform a shape, we show that it has
notation'or" . For example, if we transform the shape been
ABCD,
transformed by using the
the new image becomes
A'B'C'D'.
, TRANSLATIONS
B
A
D
D!
B'"
A
Vertical Translations
Horizontal Translations
Fill inthe following:
Fill in the following: - )
3) A(2: 3) ’ A" (24k; -
A( 2:3)’ A'(-6: B(3: 5) ’ B"( 3 i -4)
B'(-S: S)
B( 3 : S) ’
4 ) C(5 i6 ) ’ C"(5;-3)
C(S: 6) ’ C(-3 ;
-3:|) D(Si )’ D"( S ;- &)
D( S: ) - D'(
General change in words:
General change in words:
îransate 8 units lo the le Iranslate units doun
mathematically as: We can write this mathematically as:
We can write this
(xiy)(x-8 ) (xiy) x 4-1 )
horizontal shift: So, in general for any vertical shift:
So, in general for any
(xiy) (X+k : (xiy)(>c
no. of plces qou move
ko left
3 | Page