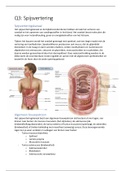
1.1 Definition of a Definite Integral
consider a function'f' defined on an interval (a, b1,
divide each ofwidth
satinto
b-a
n equal parts ax=
n
xo= a
*. Gek......b xn =
and xx a
=
k(AX)
+
on each subinterval, construct a rectangle of neigh f(X,*), for some X,*in the sub interval
subinterval
= a b
area ofthe kin rectangle is f(x,)Ax
add up the area ofall smaller rectangles getanto estimate of the desired area:
A f(X,*)AX
= + f(X,*)Ax ....
+
f(Xn*)AX
a sum of this form is called aRiemann Sum
Summation (Sigmal Notation
"f(x) 1) =
f(m) f(m + +
f(m 2)
+ +
...
+
f()
-
eg..:T =8
R
1 111 1
=
+ + +
....
+
4 n
=
.
n n times
k 1 2 3 ...+n
=
+ + +
n(n
=
1)
+
k1
Z
=
Some Summations to note:
13 I = n
= 1
2)I n(n 1)
=
+
2
3) I= n(n 1)(2n 1) +
0
+
4)
Er (1 =
v
+
rz
+ ...r)
+
r,
=
geometricsum"
Properties of Summations:
1) "Car 2
=
"an
kM =
kM
=
(a, (A2 Cay+ +
..
+
. Can) ((a,
+
=
Az 0s+...+an)
+
+
"(ax "bxz
2)
kM
=
+
bx) mak
= +
kM =
, N
for summation (2):LetS =,k 1
=
2
+
+
...+ (n -
1) n
+
x
1g
=
t x
=
(n
+ - 1) .
+
.. 2
+
+
1
25 ... (n +1) (n 1)
2
+
= +
n times
2S n(n +1)
=
S n(n 1) =
+
2
for summation (4):Let S = r 1
= +
r r2
+
...+
+ r
k 0 =
both sides by r
multiple
r8 2 r3
1
fn
+
=
.
+ +
...+
+
S-v8 fn
1
+
=1 -
1
S(1 -v) n
+
=1 -
1 1
S wn jn
+ +
=1 -
- -
I
1 -
r r
-
1
Back to Riemann Sums:
Let Rn Yf(x,*)Ax
=
-
ckth
rectangle kth rectangle
- ->
1
xx -
1
XK
a b
if x,* xx-1,
= the Reimann sum is calle "left"sum. In
a
Reimann
if X,* YK, the sum is called "right" sum. In
a
=
if Xx*:Xx-1 X, +
the Reimann sum is a "midpoint"sum, Mn
2
Definition ofa Definite integral
Saf(x) dX is defined by:
Saf(x)dx=Rn =
eif(x,Ax)
where Ax x a k(nx), and xx*
is any number [Xx-1, XxcI
ba in
= +
c
=
provided the limitexists.
"limits
of integration"
in the expression Safx)dx
"Integrand"
Iff(x) 0
< on Ca, bI, we define the area under the graph off (and above the x-axis) to be
SaPf(x)dX
examples
①
Find S,"exdx (by the definition)
y ex
=
Ax
=k
=
I
0
xx 0
= k((n)
+
=
kn
consider a function'f' defined on an interval (a, b1,
divide each ofwidth
satinto
b-a
n equal parts ax=
n
xo= a
*. Gek......b xn =
and xx a
=
k(AX)
+
on each subinterval, construct a rectangle of neigh f(X,*), for some X,*in the sub interval
subinterval
= a b
area ofthe kin rectangle is f(x,)Ax
add up the area ofall smaller rectangles getanto estimate of the desired area:
A f(X,*)AX
= + f(X,*)Ax ....
+
f(Xn*)AX
a sum of this form is called aRiemann Sum
Summation (Sigmal Notation
"f(x) 1) =
f(m) f(m + +
f(m 2)
+ +
...
+
f()
-
eg..:T =8
R
1 111 1
=
+ + +
....
+
4 n
=
.
n n times
k 1 2 3 ...+n
=
+ + +
n(n
=
1)
+
k1
Z
=
Some Summations to note:
13 I = n
= 1
2)I n(n 1)
=
+
2
3) I= n(n 1)(2n 1) +
0
+
4)
Er (1 =
v
+
rz
+ ...r)
+
r,
=
geometricsum"
Properties of Summations:
1) "Car 2
=
"an
kM =
kM
=
(a, (A2 Cay+ +
..
+
. Can) ((a,
+
=
Az 0s+...+an)
+
+
"(ax "bxz
2)
kM
=
+
bx) mak
= +
kM =
, N
for summation (2):LetS =,k 1
=
2
+
+
...+ (n -
1) n
+
x
1g
=
t x
=
(n
+ - 1) .
+
.. 2
+
+
1
25 ... (n +1) (n 1)
2
+
= +
n times
2S n(n +1)
=
S n(n 1) =
+
2
for summation (4):Let S = r 1
= +
r r2
+
...+
+ r
k 0 =
both sides by r
multiple
r8 2 r3
1
fn
+
=
.
+ +
...+
+
S-v8 fn
1
+
=1 -
1
S(1 -v) n
+
=1 -
1 1
S wn jn
+ +
=1 -
- -
I
1 -
r r
-
1
Back to Riemann Sums:
Let Rn Yf(x,*)Ax
=
-
ckth
rectangle kth rectangle
- ->
1
xx -
1
XK
a b
if x,* xx-1,
= the Reimann sum is calle "left"sum. In
a
Reimann
if X,* YK, the sum is called "right" sum. In
a
=
if Xx*:Xx-1 X, +
the Reimann sum is a "midpoint"sum, Mn
2
Definition ofa Definite integral
Saf(x) dX is defined by:
Saf(x)dx=Rn =
eif(x,Ax)
where Ax x a k(nx), and xx*
is any number [Xx-1, XxcI
ba in
= +
c
=
provided the limitexists.
"limits
of integration"
in the expression Safx)dx
"Integrand"
Iff(x) 0
< on Ca, bI, we define the area under the graph off (and above the x-axis) to be
SaPf(x)dX
examples
①
Find S,"exdx (by the definition)
y ex
=
Ax
=k
=
I
0
xx 0
= k((n)
+
=
kn