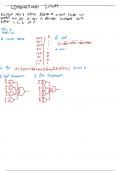Class notes for ECEN370 Digital Logic Design

Combinational Circus

Account has 3 infurs Design a circuit that its
.




output will be a one if decimal numbers are
either 1, 2, 3 or 7
, .




OR = t
AND = Xa

O
B Sup :




I
a table : 000
trvin .


001
! 2 = aic
+ 52 Fac+96L
010
I
011 Where
* I


100 8
&
101
110 g

111 V

C
. Posi (a = ++
c)(a + b +c) ( + bic)(c+ +2) Awnere o




O Sop schematic :
.
E Pos schematic

# 9


- .

,Ano-of circuits can be directly converted to NAND
by inverting one
to cropuis and OR mers.



-
Of-AND crats Can be convertedrf all her

In the same .
way



Implicant : Also called Product terms ,
all inputs are
AND ed
implicate : Also called Sum terms ,
all ineuts are
Ored
canonical term : A Product/sum from Front Includes
all in Purs
Mintern : a canonical product term
Maxterm : a canonical Sum Term


normal forms : a product/Sum torm win one
or more Inputs missing

AxioMS :

0 0 1 IH = 1 1 / : / = 0= 0 1 .
0 = 0
. = . 6 + 0

1+ 0 = 1 0 + 1 = 1 X= 0 , X=

duality : Change all and to or change all
,


Zerds to ones leave all
, inverters alone .

, Single variable Theorems X 0= 0 .
X+ 1 = 1

X .
1= X X + =X

X .
x = X X+x = X

X .
x= O x
+ Y =
1



2 and 3 Variable : YoX
X : Y=
X -y = Y+ X
X .

(x + y) = X x(yoz) = * .
y)2 (x (y 2) (+y)+ + =
+2



Xy + xy = X X .

(y+z) = xy
+ xz


x + y2 = (x y)(x + 2)
+




example : Simplify (x+ y ) (x + 2)
X
( + y((x+ 2) = X x +
.

x +
2 + X .
y + x . z

X + + Xy + Yz
I xz

=
x(y) + y2


+
=
(1) + y =

Demorgans X + yY = X + Y




Pridity : Not, Rel And Let
,
or
her