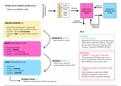
Vectoren
•Wat is een vector
→ =→ B
Notatie: vector AB u
→ →
u
Grootte: ||AB|| = |AB|
Richting: volgens de drager
Zin: pijl A
Grootte: ||u|| = |u| = √ux² + uy² (stelling van Pythagoras) y
Algebraïsch: op basis van coördinaten
Gelijke vectoren hebben: dezelfde zin, dezelfde richting en →
u
uy
dezelfde grootte
0 ux x
Tegengestelde vectoren: kunnen dezelfde grootte hebben, maar
Tegengestelde richtingen en tegengestelde zin
Soorten vectoren:
Glijdende vector:
- heeft een vaste grootte en richting, maar kan vrij bewegen over zijn drager
Gebonden vector:
- heeft een vaste grootte en richting, en ook een vast aangrijpingspunt
!Let op: teken vectoren buiten het lichaam en met als aangrijpingspunt de punt van de vector!
NIET WEL NIET WEL
, •Optellen van vectoren
→
c
Grafische methode:
→
a
- parallellogramregel (zelfde aangrijpingspunt)
- de vectorsom = de resultante
→ → →
- a + b = b +→
a =→
c →
b
→ → →
a+b+c
- herhaal de parallellogramregel
→ →
a+b
(meerdere vectoren met eenzelfde aangrijpingspunt)
→
→ b →
a → b
→
a
c
→
c
- kopstaartregel →
v
verschillend aangrijpingspunt → →
w u
→ →
u w
→
u →
v →
v
→
u +→
v=→
w =→
v +→
u
- krachtenveelhoek
kopstaartregel bij meerdere vectoren met verschillend aangrijpingspunt
→
c → →
→ →
a + b +→
c a →
c →
a + b +→ a
→ a +→
→ b +→
c
b
→ →
c b
→
b
→
a
→
c
•Wat is een vector
→ =→ B
Notatie: vector AB u
→ →
u
Grootte: ||AB|| = |AB|
Richting: volgens de drager
Zin: pijl A
Grootte: ||u|| = |u| = √ux² + uy² (stelling van Pythagoras) y
Algebraïsch: op basis van coördinaten
Gelijke vectoren hebben: dezelfde zin, dezelfde richting en →
u
uy
dezelfde grootte
0 ux x
Tegengestelde vectoren: kunnen dezelfde grootte hebben, maar
Tegengestelde richtingen en tegengestelde zin
Soorten vectoren:
Glijdende vector:
- heeft een vaste grootte en richting, maar kan vrij bewegen over zijn drager
Gebonden vector:
- heeft een vaste grootte en richting, en ook een vast aangrijpingspunt
!Let op: teken vectoren buiten het lichaam en met als aangrijpingspunt de punt van de vector!
NIET WEL NIET WEL
, •Optellen van vectoren
→
c
Grafische methode:
→
a
- parallellogramregel (zelfde aangrijpingspunt)
- de vectorsom = de resultante
→ → →
- a + b = b +→
a =→
c →
b
→ → →
a+b+c
- herhaal de parallellogramregel
→ →
a+b
(meerdere vectoren met eenzelfde aangrijpingspunt)
→
→ b →
a → b
→
a
c
→
c
- kopstaartregel →
v
verschillend aangrijpingspunt → →
w u
→ →
u w
→
u →
v →
v
→
u +→
v=→
w =→
v +→
u
- krachtenveelhoek
kopstaartregel bij meerdere vectoren met verschillend aangrijpingspunt
→
c → →
→ →
a + b +→
c a →
c →
a + b +→ a
→ a +→
→ b +→
c
b
→ →
c b
→
b
→
a
→
c