Garantie de satisfaction à 100% Disponible immédiatement après paiement En ligne et en PDF Tu n'es attaché à rien
logo-home
Recherché précédemment par vous
Recherché précédemment par vous
logo
samenvatting wiskunde rationale functies €2,99
Ajouter au panier
Accédez rapidement à
Aperçu
  2.  
  3. 3rd Degree
  4.  
  5. 3rd Degree
  6.  
  7. Wiskunde

Resume

samenvatting wiskunde rationale functies
 26 vues  0 fois vendu

In de samenvatting vind je hoofdstuk 2 : rationale functies samengevat uit het boek delta nova 5 analyse deel 1. Je kan de samenvatting ook zeker gebruiken als je een ander boek hebt. Als je ze maar nodig hebt voor rationale functies.

Aperçu 1 sur 2  pages

Infos sur le Document

  • Non
  • Hoofdstuk 2
  • 1 juin 2022
  • 2
  • 2021/2022
  • Resume

Sujets

Livre connecté

book image

Titre de l’ouvrage:

Auteur(s):

  • Édition:
  • ISBN:
  • Édition:

Plus de résumés pour

Tout pour ce livre (8)

École, étude et sujet

  • Lycée
  • 3rd degree
  • Wiskunde
  • 5
Tous les documents sur ce sujet (15)

Vendeur

avatar-seller
hannevanlandeghem

Avis reçus

Aperçu du contenu

H2 RATIONALE FUNCTIES

2.1 DOMEIN, NULPUNTEN EN TEKENONDERZOEK

2.1.1 RATIONALE FUNCTIES, DOMEIN EN NULPUNTEN

Definitie rationale functie Is een functie met een voorschrift van de vorm
t (x )
f(x) =
r ( x)
n n−1
Algemeen voorschrift an x + an−1 x +…+ a1 x +a 0
F(x) = m m−1
bm x + bm−1 x + …+b1 x+b 0
Gebroken rationale functie Een rationale functie die geen veeltermfunctie
is
Domein Is de verzameling van alle reële getallen die
geen nulpunten zijn van de nummer, want een
breuk is enkel bepaald als de noemer
verschillend is van 0
nulpunten Zijn de nulpunten van de teller die geen
nulpunten van de noemer zijn, want een breuk
is 0 als de teller gelijk is aan 0 en de noemer
verschillend is van 0
2.1.2 TEKENONDERZOEK

Normaal gezien doe je maal maar nu Deel je
2.2 VERTICALE ASYMPTOTEN EN OPENINGEN

2.2.1 GEDRAG VAN DE GRAFIEK IN DE BEURT VAN EEN NULPUNT VAN DE NOEMER

Asymptoot definitie De recht met vergelijking x=a is een verticale
asymptoot van de grafiek van f
⇕
Als x -> a dan f(x) -> ± ∞
Opening In het punt (a,b) is een opening van de grafiek
van f
⇕
Als x -> a dan f(x) -> b(b∈ R )
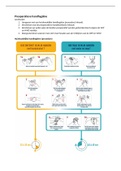
2.2.2 VERTICALE ASYMPTOTEN EN OPENINGEN UIT HET VOORSCHRIFT AFLEIDEN

Volgorde voor het bepalen van een opening en - Is a een nulpunt van de noemer en niet
asymptoten van de teller -> verticale asymptoot
- Is a een nulpunt van de noemer en de
teller -> vereenvoudig het voorschrift zo
ver mogelijk het resultaat is g(x)
 Is a GEEN nulpunt van de noemer ->
opening
 Is a een nulpunt van de noemer ->
verticale asymptoot
Vereenvoudigd voorschrift x
F(x) = mits x≠ (nulpunt noemer en teller)
x−1
Hoe ontbind je een 4de macht x + x +1= a( x + x 1)( x - x 2)
4 2 2 2

Les avantages d'acheter des résumés chez Stuvia:

Qualité garantie par les avis des clients

Qualité garantie par les avis des clients

Les clients de Stuvia ont évalués plus de 700 000 résumés. C'est comme ça que vous savez que vous achetez les meilleurs documents.

L’achat facile et rapide

L’achat facile et rapide

Vous pouvez payer rapidement avec iDeal, carte de crédit ou Stuvia-crédit pour les résumés. Il n'y a pas d'adhésion nécessaire.

Focus sur l’essentiel

Focus sur l’essentiel

Vos camarades écrivent eux-mêmes les notes d’étude, c’est pourquoi les documents sont toujours fiables et à jour. Cela garantit que vous arrivez rapidement au coeur du matériel.

Foire aux questions

Qu'est-ce que j'obtiens en achetant ce document ?

Vous obtenez un PDF, disponible immédiatement après votre achat. Le document acheté est accessible à tout moment, n'importe où et indéfiniment via votre profil.

Garantie de remboursement : comment ça marche ?

Notre garantie de satisfaction garantit que vous trouverez toujours un document d'étude qui vous convient. Vous remplissez un formulaire et notre équipe du service client s'occupe du reste.

Auprès de qui est-ce que j'achète ce résumé ?

Stuvia est une place de marché. Alors, vous n'achetez donc pas ce document chez nous, mais auprès du vendeur hannevanlandeghem. Stuvia facilite les paiements au vendeur.

Est-ce que j'aurai un abonnement?

Non, vous n'achetez ce résumé que pour €2,99. Vous n'êtes lié à rien après votre achat.

Peut-on faire confiance à Stuvia ?

4.6 étoiles sur Google & Trustpilot (+1000 avis)

50402 résumés ont été vendus ces 30 derniers jours

Fondée en 2010, la référence pour acheter des résumés depuis déjà 15 ans

Commencez à vendre!
€2,99
  • (0)
Ajouter au panier
Ajouté