1 Mathematics
1.1 Sets and Functions
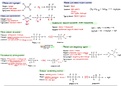
Definition 1. A consumption set, X, is said to be convex if and only if for every x, y, z 2 X,
where y ⌫ x and z ⌫ x we have for every q 2 [0, 1]
qy + (1 q )z ⌫ x. (1)
The term ‘convex preferences’ refers to the convexity of consumers’ consumption sets.
Convex preferences imply:
1. =) concave utility functions.
2. =) convex indifference curves.
Convex preferences are a fundamental assumption of many economic models.
1.2 Calculus
1.2.1 Di↵erentiation
Definition 2. Implicit differentiation provides a way to differentiate when two variables x
and y are implicitly related through z( x, y) = c.
In the case where z( x, y) = 0, we have:
∂z ∂z
dz = dx + dy = 0. (2)
∂x ∂y
which through rearranging will give us the derivative of y with respect to x:
∂z
dy
= ∂x
. (3)
dx ∂z
∂y
1.2.2 Integration
Definition 3. Integration by parts has the formula
Z Z
f 0 ( x ) g( x )dx = f ( x ) g( x ) f ( x ) g0 ( x )dx. (4)
Definition 4. Integration by substitution has the formula
Z
f 0 ( g( x )) g0 ( x )dx = f ( g( x )) + c. (5)
7
, 1.3 Optimisation
1.3.1 Quasi-concavity
Definition 5. A function f is said to be quasi-concave if for any ( x, x 0 ) where x 6= x 0 and
f ( x ) = f ( x 0 ) we have
f (tx + (1 t) x0 ) > f ( x ) = f ( x0 ) , t 2 (0, 1). (6)
• Critical points on a quasi-concave function are global maxima.
1.3.2 Transformation
Minimisation problems can be converted into maximisation problems by using the fact
that
min f ( x, y) , max f ( x, y). (7)
1.3.3 Multi-variate Optimisation
In order for a critical point ( x0 , y0 ) on f ( x, y) to be a global maximum we need the
first-order conditions to hold:
∂f
1. ∂x ( x0 , y0 ) = 0.
∂f
2. ∂y ( x0 , y0 ) = 0.
However, these conditions are insufficient for maximisation. Further, we need the sec-
ond partial derivatives to be negative for concavity:
∂2 f
1. ∂x2
( x0 , y0 ) < 0.
∂2 f
2. ∂y2
( x0 , y0 ) < 0.
But we need one further condition. Even if these four conditions hold, we might still
find a saddle point rather than a global optimum.
8
1.1 Sets and Functions
Definition 1. A consumption set, X, is said to be convex if and only if for every x, y, z 2 X,
where y ⌫ x and z ⌫ x we have for every q 2 [0, 1]
qy + (1 q )z ⌫ x. (1)
The term ‘convex preferences’ refers to the convexity of consumers’ consumption sets.
Convex preferences imply:
1. =) concave utility functions.
2. =) convex indifference curves.
Convex preferences are a fundamental assumption of many economic models.
1.2 Calculus
1.2.1 Di↵erentiation
Definition 2. Implicit differentiation provides a way to differentiate when two variables x
and y are implicitly related through z( x, y) = c.
In the case where z( x, y) = 0, we have:
∂z ∂z
dz = dx + dy = 0. (2)
∂x ∂y
which through rearranging will give us the derivative of y with respect to x:
∂z
dy
= ∂x
. (3)
dx ∂z
∂y
1.2.2 Integration
Definition 3. Integration by parts has the formula
Z Z
f 0 ( x ) g( x )dx = f ( x ) g( x ) f ( x ) g0 ( x )dx. (4)
Definition 4. Integration by substitution has the formula
Z
f 0 ( g( x )) g0 ( x )dx = f ( g( x )) + c. (5)
7
, 1.3 Optimisation
1.3.1 Quasi-concavity
Definition 5. A function f is said to be quasi-concave if for any ( x, x 0 ) where x 6= x 0 and
f ( x ) = f ( x 0 ) we have
f (tx + (1 t) x0 ) > f ( x ) = f ( x0 ) , t 2 (0, 1). (6)
• Critical points on a quasi-concave function are global maxima.
1.3.2 Transformation
Minimisation problems can be converted into maximisation problems by using the fact
that
min f ( x, y) , max f ( x, y). (7)
1.3.3 Multi-variate Optimisation
In order for a critical point ( x0 , y0 ) on f ( x, y) to be a global maximum we need the
first-order conditions to hold:
∂f
1. ∂x ( x0 , y0 ) = 0.
∂f
2. ∂y ( x0 , y0 ) = 0.
However, these conditions are insufficient for maximisation. Further, we need the sec-
ond partial derivatives to be negative for concavity:
∂2 f
1. ∂x2
( x0 , y0 ) < 0.
∂2 f
2. ∂y2
( x0 , y0 ) < 0.
But we need one further condition. Even if these four conditions hold, we might still
find a saddle point rather than a global optimum.
8