Basis
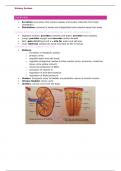
r e i∗φ =r ( cos ( φ ) +isin ( φ ))r =||φ=arg Tekenen
|z|=… cirkel met straal ... met middelpunt 0 (passer!)
|z +? ? ?−‼! i|=… cirkel met straal ... en middelpunt (-???, + !!!i)
vb: |z +2−i| middelpunt (-2, i)
Im(z) = horizontale lijn bij bepaalde i-waarde
Re(z) = verticale lijn bij bepaalde normale waarde
Krijg je iets als Re(z) +Im(z) = ... dan moet je een tabel maken met 2 punten die daar aan voldoen en
daar dan een rechte lijn doorheen tekenen
2
z∗z=|z| Vb: z∗z=5 is cirkel met middelpunt 0 en straal √ 5
Differentievergelijkingen
1. Substitutie van gn in un:
2
un=2u n−1 −2u n−2 → g =2 g−2
2. Oplossen met kwadraatafspliten
Vb g = 1 + i V g = 1 – i
3. Bereken modelus en argument
|1+i|= √2 arg(1 + i) = 1/4π
4. Gebruik de formule un=( Acos ( φn ) + Bsin ( φn ) )∗gn , hierbijis φ het argument en g de modules
un= Acos ( 14 π n)+ Bsin( 14 π n)∗¿
5. Vul de waardes van u0 en u1 in
u0 = 2 geeft automatisch je A getal dus A = 2
u1 = 5 geeft:
5=(2 cos ( 14 π )+ Bsin( 41 π ))∗¿5=(√ 2+ B∗1
2
√ 2)∗√ 25=2+ BB=3
dus :un=2 cos ( π n ) +3 sin ( π n)∗¿
1 1
4 4
n
Niet complex ? un=A∗g 1 + B∗g 2 , g zijn oplossingen met abc 1 oplossing ? un=( A + Bn ) g
n n
Complexe wortels
1. Berken de modules en argument
2. Zet in de vorm: r e i∗φ+k∗2 π
3. Ga door met k’s invoeren tot dat de macht ophoudt
vb bij z2 gebruik k = 0 en k =1 en bij z3 gebruik je k = 0, k = 1 en k = 2 enzovoort
r e i∗φ =r ( cos ( φ ) +isin ( φ ))r =||φ=arg Tekenen
|z|=… cirkel met straal ... met middelpunt 0 (passer!)
|z +? ? ?−‼! i|=… cirkel met straal ... en middelpunt (-???, + !!!i)
vb: |z +2−i| middelpunt (-2, i)
Im(z) = horizontale lijn bij bepaalde i-waarde
Re(z) = verticale lijn bij bepaalde normale waarde
Krijg je iets als Re(z) +Im(z) = ... dan moet je een tabel maken met 2 punten die daar aan voldoen en
daar dan een rechte lijn doorheen tekenen
2
z∗z=|z| Vb: z∗z=5 is cirkel met middelpunt 0 en straal √ 5
Differentievergelijkingen
1. Substitutie van gn in un:
2
un=2u n−1 −2u n−2 → g =2 g−2
2. Oplossen met kwadraatafspliten
Vb g = 1 + i V g = 1 – i
3. Bereken modelus en argument
|1+i|= √2 arg(1 + i) = 1/4π
4. Gebruik de formule un=( Acos ( φn ) + Bsin ( φn ) )∗gn , hierbijis φ het argument en g de modules
un= Acos ( 14 π n)+ Bsin( 14 π n)∗¿
5. Vul de waardes van u0 en u1 in
u0 = 2 geeft automatisch je A getal dus A = 2
u1 = 5 geeft:
5=(2 cos ( 14 π )+ Bsin( 41 π ))∗¿5=(√ 2+ B∗1
2
√ 2)∗√ 25=2+ BB=3
dus :un=2 cos ( π n ) +3 sin ( π n)∗¿
1 1
4 4
n
Niet complex ? un=A∗g 1 + B∗g 2 , g zijn oplossingen met abc 1 oplossing ? un=( A + Bn ) g
n n
Complexe wortels
1. Berken de modules en argument
2. Zet in de vorm: r e i∗φ+k∗2 π
3. Ga door met k’s invoeren tot dat de macht ophoudt
vb bij z2 gebruik k = 0 en k =1 en bij z3 gebruik je k = 0, k = 1 en k = 2 enzovoort