Calculus Early Transcendentals
15th Edition By Joel Hass,
Christopher Heil, Maurice Weir,
Przemyslaw Bogacki (All Chapters
1-19, 100% Original Verified, A+
Grade)
All Chapters Arranged Reverse:
Chapter 19-1
This is the Original Solutions
Manual for 15th Edition, All Other
Files in the Market are Wrong/Old
Questions.
, CHAPTER 19 FOURIER SERIES AND WAVELETS
19.1 PERIODIC FUNCTIONS
1. 2 2. Not periodic
3. Not periodic 4. 2
5. 2 6. Not periodic
7. (a) Since f x P f x and g x P g x for every x, it follows that
f x P g x P f x g x for every x.
8. If y is a real number, then y x 2k for some 0 x 2 and integer k . Then y 2 x 2k 1 , so
f y 2 f x 2k 1 f x f x 2k f y . Therefore f has period 2 .
19.2 SUMMING SINES AND COSINES
1. This follows from the fact that sin kx sin kx.
2. This follows from the fact that cos kx sin kx.
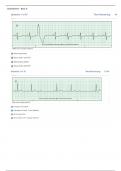
3. The graphs of p5 and p13 are shown in the accompanying figure. It appears that pn is converging to the
x, 0 x ,
function f whose values on the domain 0, 2 are f x
2 x , x 2 ,
with these values then repeated every 2 units. The convergence is “fast” since the graph of pn is already
close to the graph of f when n is small.
4. The graphs of p3 , p7 , and p21 are shown in the accompanying figure. It appears that pn is converging to
1, x 3 ,
the function f whose values on the domain 0, 2 are f x
2 2
3
0, 0 x 2 or 2 x 2 ,
with these values then repeated every 2 units. The convergence is “slow” since we must take n fairly large
before the graph of pn appears to be close to the graph of f .
Copyright 2023 Pearson Education, Inc.
1323
,1324 Chapter 19 Fourier Series and Wavelets
5. z 0 cos 0 x i sin 0 x 1
6. z 1 i cos x i sin x 1 i 1 cos x i 1 sin x
7. 2 z 2 3z 5 2 ei 2 x 3 ei x 5 2 cos 2 x i sin 2 x 3 cos x i sin x 5
n n n
8. ak z k ak ei kx ak cos kx i sin kx
k 0 k 0 k 0
1
9. z 1 ei x e i x cos x i sin x cos x i sin x
n
e cos n x i sin n x cos nx i sin nx
i n x
10. z n ei x
11. z z 1 cos x i sin x cos x i sin x 2 cos x
12. z z 1 cos x i sin x cos x i sin x 2 i sin x
13. z n z n cos nx i sin nx cos nx i sin nx 2 cos nx
14. z n z n cos nx i sin nx cos nx i sin nx 2 i sin nx
15. 2 z 2 3z 5 3z 1 2 z 2 2 z 2 z 2 3 z z 1 5 2 2 cos 2 x 3 2 cos x 5
16. 4 iz 2 2 iz 2 iz 1 4 iz 2 4 i z 2 z 2 2 i z z 1 4 i 2 i sin 2 x 2 i 2 i sin x 8sin 2 x 4sin x
Copyright 2023 Pearson Education, Inc.
, Section 19.3 Vectors and Approximation in Three and More Dimensions 1325
17. cos x 2sin x 3 1
2 z z 1 i z z 1 3 0.5 i z 3 0.5 i z 1
18. 2 cos 3x 6 cos 2 x 8sin 3 x 5 z 3 z 3 3 z 2 z 2 4i z 3 z 3 5
1 4i z 3 3z 2 5 3z 2 1 4i z 3
19.3 VECTORS AND APPROXIMATION IN THREE AND MORE DIMENSIONS
1. (a) r s 0, r t 0, s t 0 (b) r 2, s 2, t 1
(c) Yes (d) No
2. (a) r s 0, r t 0, s t 0 (b) r 1, s 1, t 1
(b) Yes (d) Yes
3. (a) r s 0, r t 0, s t 3 (b) r 3, s 6, t 2
(b) No (d) No
3
4. (a) r s 0, r t 0, s t 2
(b) r 1, s 1, t 1
(b) No (d) No
5. (a) r s 0, r t 0, s t 0 (b) r 1, s 1, t 1
(b) Yes (d) Yes
6. (a) r s 0, r t 0, s t 0 (b) r 1, s 1, t 1
(c) Yes (d) Yes
7. (b) p 1, 2, 0 (c) 3
8. (b) p 1, 4, 1 (c) 6
9. (b) p 7 , 1 ,1 (c) 3
2 2 2
10. (b) p 9,9,3 7 (c) 4
5 5 5
11. 2u v 3w 6, 4, 7,8,1 , u 5v w 10, 6, 4, 7, 3
12. u 3 2, v 2, w 4
13. u v 6, u w 3, v w 1
14. 63, 27, 51,39, 12
15. u j u k 0 when j k , and u k 1 for k 1, 2,3, 4,5
16. p v u1 u1 1, 1, 0, 0, 0 , v p 39 6.24, v p u1 0
Copyright 2023 Pearson Education, Inc.